
Pessoas não familiarizadas com sistemas de controle digital acreditam que quanto maior a taxa de amostragem, melhor a fidelidade do controle. É verdade que a fidelidade de controle melhora com o aumento da taxa de amostragem, mas apenas até um certo ponto. Além desse ponto, o controle é essencialmente analógico, e não ocorre mais nenhuma melhoria. Se a taxa de amostragem for aumentada ainda mais, a fidelidade de controle na verdade se degrada devido aos efeitos numéricos prejudiciais, tais como quantificação de coeficiente e erro de roundoff.
Como será demonstrado neste relatório, a regra geral para sistemas servo-hidráulicos é que a taxa ideal de amostragem seja cinquenta vezes a largura de banda do sistema, definida como a frequência natural da coluna de óleo (ou qualquer outro modo dinâmico dominante). A largura de banda da maioria dos sistemas servo-hidráulicos MTS é de 100 Hz ou menos, portanto, uma taxa de amostragem de 100 x 50 = 5 kHz é suficiente. Além desta taxa de amostragem, há pouca ou nenhuma melhoria na fidelidade de controle.
A taxa de amostragem na qual o controle se degrada devido aos efeitos numéricos é difícil de determinar, pois depende de muitos fatores tais como precisão numérica, amplitude e largura da banda do sinal, frequências de quebra do filtro digital, etc. Ele só pode ser descoberto por meio de testes exaustivos (ou seja, caros).
Aumentar a taxa de amostragem além do ponto ideal aumenta o custo do hardware em tempo real. Também há um custo de oportunidade perdida: uma vez que grande parte da largura de banda do processador em tempo real é desperdiçada em cálculos que não melhoram a fidelidade do controle, há pouca largura de banda restante para algoritmos de controle avançados que melhoram a fidelidade, como o Controle Inverso Adaptativo (AIC).
Este relatório limita a discussão para controlar a taxa de amostragem. Existem outras taxas de amostragem em um controlador, tais como a taxa de amostragem de aquisição de dados. Pode haver boas razões para ter uma taxa de amostragem de aquisição de dados muito maior do que a do controlador de loop fechado.
Os seguintes tópicos são considerados:
- Controlar a fidelidade como uma função da taxa de amostragem
- Controle de fidelidade como uma função da latência (definido como o número de amostras de atraso entre a leitura de feedbacks de sensores e a gravação de comandos de servoválvulas)
- Efeitos numéricos
As conclusões alcançadas neste relatório estão resumidas aqui:
- A taxa ideal de amostragem de controle para a maioria dos sistemas servo-hidráulicos MTS é de 5 kHz. Taxas de amostragem mais altas têm pouco ou nenhum benefício.
- A obtenção de taxas de amostragem mais altas por meio do compartilhamento de carga entre vários processadores em tempo real aumenta a latência, o que degrada significativamente a fidelidade do controle.
A fidelidade de controle foi analisada usando análise de resposta de frequência de um sistema servo-hidráulico típico de várias larguras de banda, taxas de amostragem e latências, e comparação:
- Resposta de frequência em loop fechado
- Resposta de frequência de interferência
- Métricas de estabilidade em loop aberto:frequências de ganho unitário e de crossover de -180 graus
O modelo do sistema servo-hidráulico apresentava as seguintes características:
- O atuador hidráulico foi um projeto "padrão" utilizado durante anos para desenvolver ferramentas analíticas e de modelagem Simulink.
- A carga útil era apenas em massa, com a massa variando para obter frequências de coluna de óleo (larguras de banda) de 25, 50, e 100 Hz.
- A largura de banda do Servovalve foi limitada a 2X da largura de banda de carga útil.
- A largura de banda de condicionamento de retorno foi ajustada para 10X da largura de banda de carga útil.
- O modo de controle era o deslocamento.
- O algoritmo de controle Proporcional Integral Derivativo (PID) com ajuste otimizado para cada largura de banda de carga útil, taxa de amostragem e latência usando um ajustador automático. Ganhos otimizados incluídos: ganho proporcional no erro de deslocamento; ganho de estabilização delta-p; frequência de corte delta-p de alta passagem.
Para mais detalhes sobre este modelo servo-hidráulico, consulte os arquivos Actuator Model.pdf, Actuator Transfer Functions.pdf, e PID Transfer Functions.pdf
Controle a fidelidade (como função da taxa de amostragem)
Para determinar o efeito da taxa de amostragem sobre a fidelidade do controle, o sistema foi analisado com taxas de amostragem de controle de 2 kHz, 5 kHz, 10 kHz e 20 kHz e larguras de banda de 25 Hz, 50 Hz e 100 Hz. A latência foi a menor possível:1,5 período de amostragem do controlador. As comparações de resposta em loop fechado, interferência e resposta em frequência de loop aberto aparecem nas páginas seguintes.
As parcelas mostram claramente que a maior parte do benefício do aumento da taxa de amostragem é obtida ao aumentar a taxa de amostragem de 2 kHz para 5 kHz. Além disso, há poucas melhorias a serem alcançadas.
Efeitos da taxa de amostragem em um sistema com largura de banda de 25 Hz
A resposta de frequência em loop fechado é otimizada um pouco (mais plana) quando a taxa de amostragem aumenta de 2 kHz para 5 kHz. Além disso, há poucas melhorias:
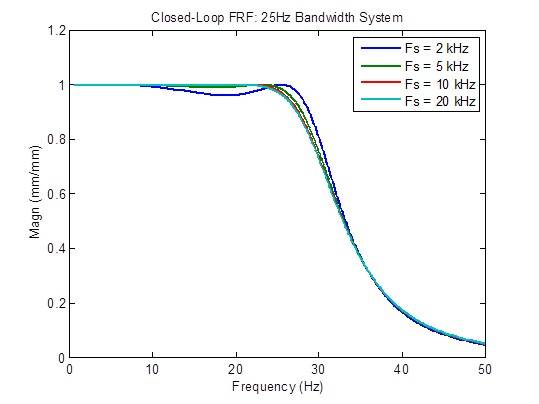
A resposta de interferência é otimizada um pouco (reduzida) quando a taxa de amostragem é aumentada de 2 kHz para 5 kHz. Além disso, há poucas melhorias:
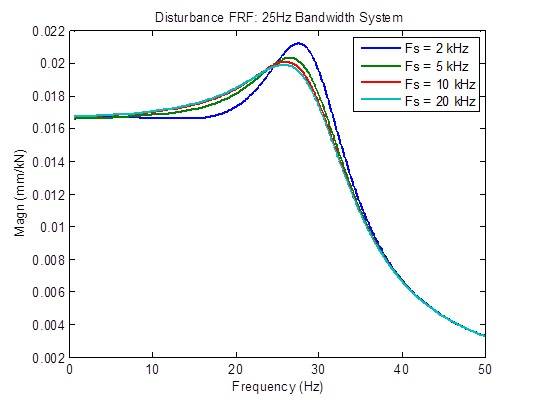
Há uma leve redução no pico de resposta de frequência em loop aberto quando a taxa de amostragem é aumentada de 2 kHz para 5 kHz. Além disso, há poucas melhorias. Em sua maioria, as métricas de estabilidade (frequências de cruzamento) não se alteram:
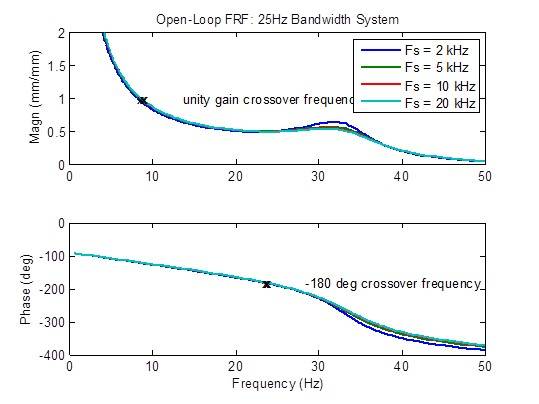
Efeitos da taxa de amostragem em um sistema com largura de banda de 50 Hz
A resposta de frequência em loop fechado é ligeiramente otimizada (mais plana) quando a taxa de amostragem aumenta de 2 kHz para 5 kHz. Além disso, há poucas melhorias:
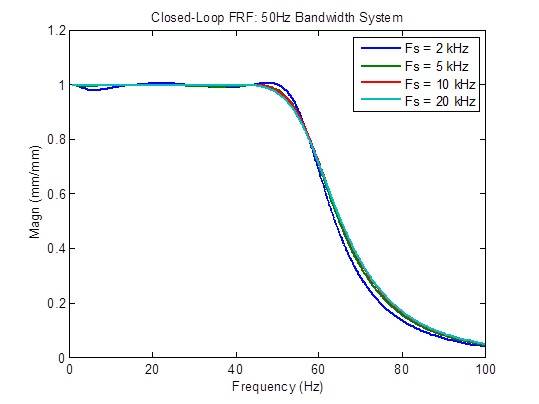
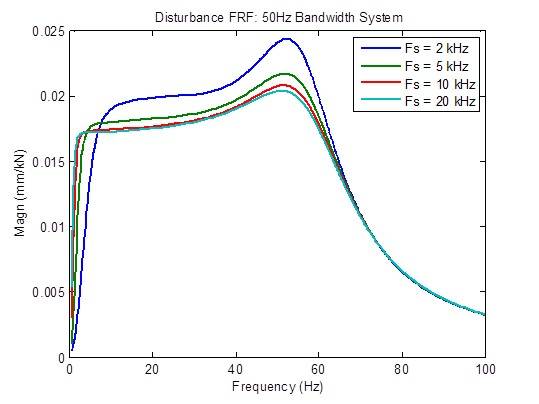
A resposta de interferência é otimizada moderadamente (reduzida) quando a taxa de amostragem é aumentada de 2 kHz para 5 kHz e otimizada um pouco quando a taxa de amostragem é aumentada de 5 kHz para 10 kHz. Além disso, há poucas melhorias:
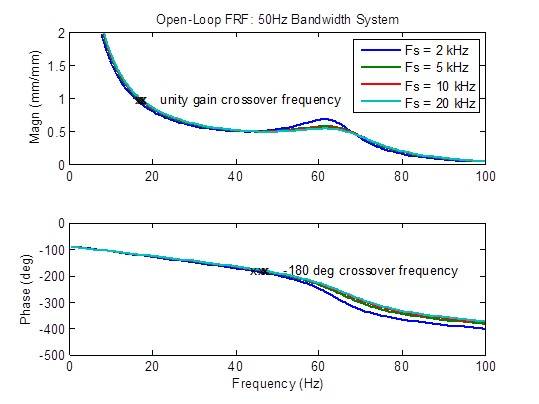
Há uma leve redução no pico de resposta de frequência em loop aberto quando a taxa de amostragem é aumentada de 2 kHz para 5 kHz. As métricas de estabilidade (frequências cruzadas) também são um pouco melhoradas (frequência mais alta). Além disso, há poucas melhorias:
Efeitos da taxa de amostragem em um sistema com largura de banda de 100 Hz
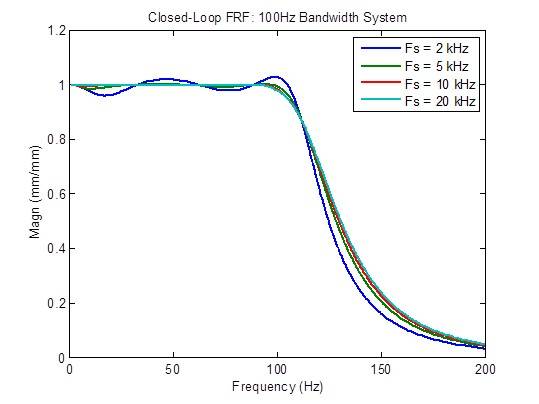
A resposta de frequência em loop fechado é significativamente otimizada (mais plana) quando a taxa de amostragem aumenta de 2 kHz para 5 kHz. Além disso, há poucas melhorias:
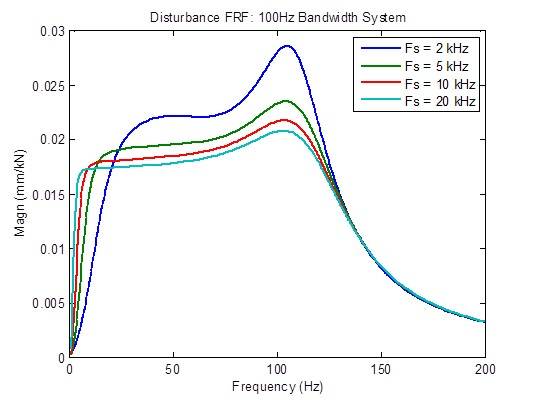
A resposta de interferência é moderadamente otimizada (reduzida) quando a taxa de amostragem é otimizada de 2 kHz para 5 kHz e um pouco melhorada quando alterada de 5 kHz para 10 kHz. Além disso, há poucas melhorias:
Há uma redução moderada no pico de resposta de frequência em loop aberto quando a taxa de amostragem é aumentada de 2 kHz para 5 kHz. As métricas de estabilidade (frequências cruzadas) também são um moderadamente melhoradas (frequência mais alta).Além disso, há poucas melhorias:
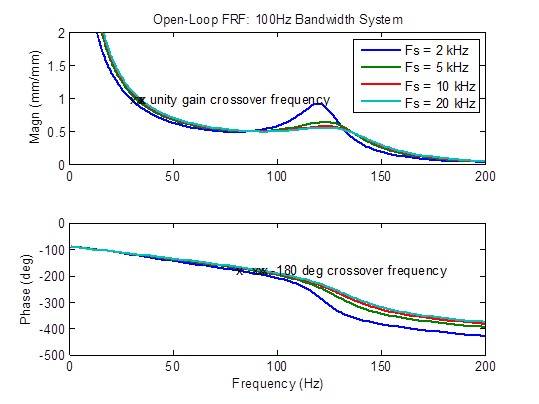
Controle a fidelidade (como função da latência)
Aumentar a taxa de amostragem vai, em algum momento, sobrecarregar um único processador em tempo real. Este problema pode ser resolvido adicionando mais processadores e repartindo a carga computacional entre eles.
Entretanto, o compartilhamento de carga aumenta a latência, que é definida como o número de amostras de atraso entre a leitura de feedbacks de sensores e a gravação de comandos de servoválvulas, de acordo com a fórmula
Latência (amostras) = número de processadores + 0.5
O valor 0,5 é um atraso devido à conversão digital para analógico. A latência mínima possível é de 1,5 amostra, o que ocorre quando apenas um processador está presente. A latência devida ao número de processadores surge devido à necessidade de sincronizar a passagem de dados de sinal de um processador para o próximo.
Para determinar o efeito da latência na fidelidade do controle, foi analisado um sistema com 100 Hz de largura de banda e uma taxa de amostragem de 10 kHz com latências de 1,5, 4, e 10 amostras. As comparações de resposta em loop fechado, interferência e resposta em frequência de loop aberto aparecem nas páginas seguintes.
As parcelas abaixo mostram claramente que a fidelidade de controle se degrada significativamente quando a latência é aumentada além do mínimo de 1,5 amostras. Isto demonstra que adicionar processadores para alcançar uma alta taxa de amostragem não é necessariamente uma coisa boa, e que pode ser melhor usar uma taxa de amostragem mais baixa que esteja dentro da capacidade de um único processador.
Observação: A razão pela qual a taxa de amostragem de 10 kHz e uma latência máxima de 10 amostras foi escolhida para esta análise é porque estas são as especificações de um controlador oferecido por um concorrente da MTS. Os gráficos finais nesta seção comparam o controlador deste concorrente com um controlador que tem a taxa de amostragem ideal de 5 kHz e a latência mínima de 1,5 amostra; o controlador do concorrente é claramente inferior.
Efeitos da latência em um sistema com largura de banda de 100 Hz com uma taxa de amostragem de 10 kHz
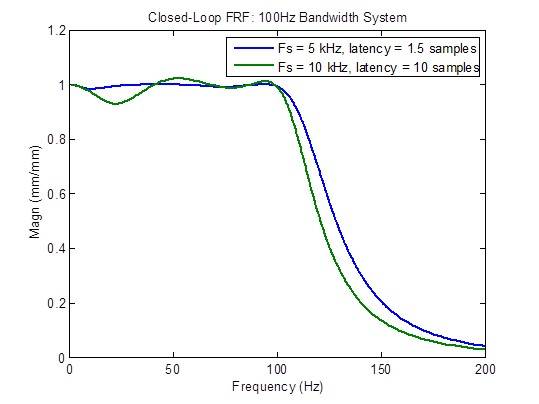
A resposta de frequência em loop fechado se degrada (torna-se menos plana) consideravelmente quando a latência é maior que o mínimo de 1,5 amostra:
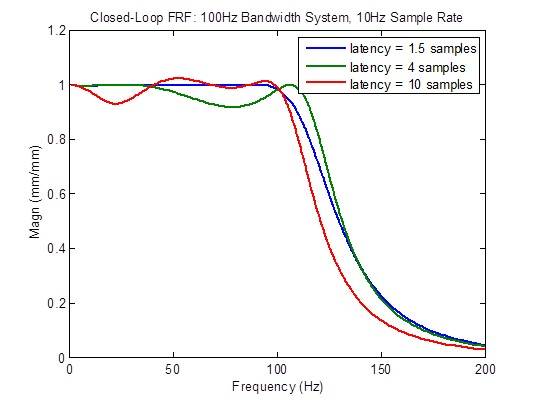
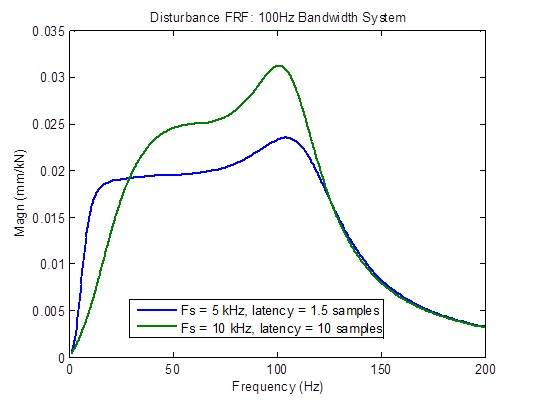
A resposta de interferência se degrada (torna-se mais alta) consideravelmente quando a latência é maior que o mínimo de 1,5 amostra. Entretanto, há uma melhoria em baixas frequências devido a razões desconhecidas neste momento:
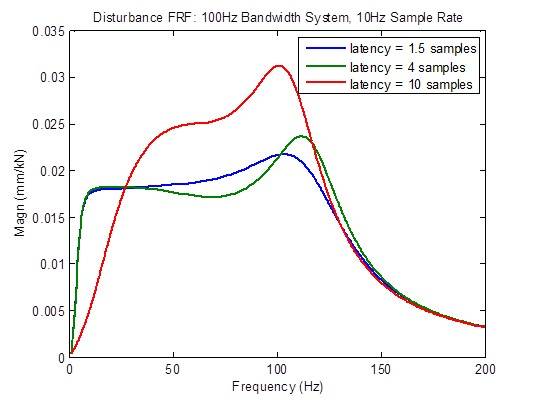
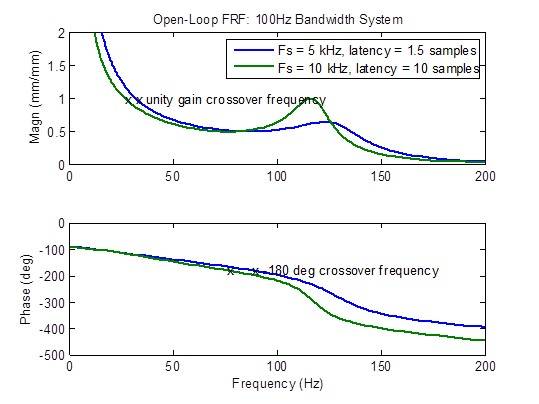
A resposta de frequência em loop aberto se degrada (cria picos) consideravelmente quando a latência é maior que o mínimo de 1,5 amostra. As métricas de estabilidade (frequências cruzadas) se degradam (ocorrem em frequências mais baixas) consideravelmente:
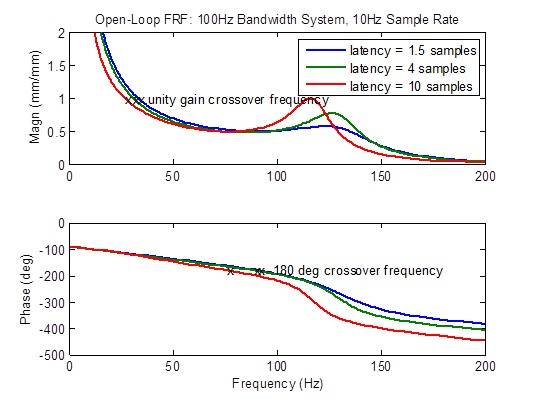
Comparação entre um sistema com largura de banda de 100 Hz com taxa de amostragem de 10 kHz com alta latência e um sistema com taxa de amostragem de 5 kHz com latência mínima
Um concorrente da MTS afirma ter um controlador com taxa de amostragem de 10 kHz com latência de 1 milissegundo (10 amostras a 10 kHz). Os gráficos de frequência abaixo mostram claramente uma resposta inferior em todos os aspectos em comparação com uma taxa de amostragem de 5 kHz com latência mínima (1,5 amostra): largura de banda reduzida, resposta de frequência não plana em loop fechado, resposta de interferência mais alta e margens de estabilidade degradadas.
Efeitos numéricos
Os efeitos numéricos prejudiciais, como a quantificação do coeficiente e do erro roundoff, pioram com o aumento da taxa de amostragem e se manifestam de várias maneiras:
Os processos de integração têm taxas de integração imprevisíveis ou podem ficar presos: Exemplos de tais processos incluem geradores de funções de rampa e integradores de controladores PID. Tomando como exemplo a geração de rampa, a fórmula abaixo gera um valor de rampa no tempo k adicionando um valor delta Δ = taxa de integração / taxa de amostragem ao resultado anterior no tempo k - 1:
yk = yk-1 + Δ
| 1 kHz | 10 kHz | 100 kHz | |
| a1 = -1,991114 | a1 = -1,999111 | a1 = -1,999911 | |
| a2 = 0,991154 | a2 = 0,999112 | a2 = 0,999911 | |
Somente os coeficientes aa 1 e a2 são de interesse, pois são eles que determinam a estabilidade e são mais suscetíveis a erros de roundoff e efeitos de quantificação. Observe que à medida que a taxa de amostragem aumenta, o número de dígitos que não são 9 diminui. Isto significa que há muito menos dígitos que definem a resposta do filtro. Eventualmente, à medida que a taxa de amostragem aumenta ainda mais, o coeficiente a1 aproxima-se de um valor de -2,0 e a2 aproxima-se de um valor de 1,0. Em algum momento, a quantificação do coeficiente de filtragem poderia resultar em um filtro cuja resposta de frequência seja errática ou mesmo instável, onde a saída oscila com grande valor mesmo com entrada zero.

