
Le persone che non hanno familiarità con i sistemi di controllo digitale credono che maggiore è la frequenza di campionamento, migliore è la fedeltà del controllo.È vero che la fedeltà del controllo migliora con l'aumento della frequenza di campionamento, ma solo fino a un certo punto. Oltre quel punto, il controllo è essenzialmente analogico e non si verificano ulteriori miglioramenti.Se la frequenza di campionamento viene ulteriormente aumentata, la fedeltà del controllo si riduce effettivamente a causa di effetti numerici dannosi come la quantizzazione del coefficiente e l'errore di arrotondamento.
Come verrà dimostrato in questo rapporto, la regola pratica per i sistemi servoidraulici è che la frequenza di campionamento ottimale sia cinquanta volte la larghezza di banda del sistema, definita come frequenza naturale della colonna d'olio (o qualsiasi altra modalità dinamica dominante). La larghezza di banda della maggior parte dei sistemi servoidraulici MTS è di 100 Hz o meno, quindi una frequenza di campionamento di 100 x 50 = 5kHz è sufficiente. Al di là di questa frequenza di campionamento, non si verifica alcun miglioramento significativo nella fedeltà del controllo.
La frequenza di campionamento alla quale il controllo si degrada a causa degli effetti numerici è difficile da determinare, poiché dipende da molti fattori come la precisione numerica, l'ampiezza e la larghezza di banda del segnale, le frequenze di rottura del filtro digitale, ecc. Può essere trovata solo con test esaustivi (cioè costosi).
L'aumento della frequenza di campionamento oltre il punto ottimale accresce il costo dell'hardware in tempo reale. Inoltre c'è un costo relativo all'opportunità persa: poiché gran parte della larghezza di banda del processore in tempo reale viene sprecata in calcoli che non migliorano la fedeltà del controllo, rimane poca larghezza di banda per algoritmi di controllo avanzati che migliorano la fedeltà, come Adaptive Inverse Control (AIC).
Questo rapporto limita la discussione per controllare la frequenza di campionamento. Ci sono altre frequenze di campionamento in un controller, come la frequenza di campionamento di acquisizione dati. Possono esserci buone ragioni per avere una frequenza di campionamento di acquisizione dati molto più elevata rispetto a quella del controller ad anello chiuso.
Vengono considerati i seguenti argomenti:
- Fedeltà del controllo in funzione della frequenza di campionamento
- Fedeltà del controllo in funzione della latenza (definita come il numero di campioni di ritardo tra la lettura dei feedback dei sensori e la scrittura dei comandi delle servovalvole)
- Effetti numerici
Le conclusioni raggiunte in questo rapporto sono riassunte di seguito:
- La frequenza di campionamento ottimale per la maggior parte dei sistemi servoidraulici MTS è di 5 kHz.Frequenze di campionamento più elevate producono benefici minimi o nulli.
- Ottenere frequenze di campionamento più elevate tramite la condivisione del carico tra più processori in tempo reale aumenta la latenza, riducendo significativamente la fedeltà del controllo.
La fedeltà del controllo è stata analizzata utilizzando l'analisi della risposta in frequenza di un tipico sistema servoidraulico di varie larghezze di banda, frequenze di campionamento e latenze e confrontando:
- Risposta in frequenza ad anello chiuso
- Risposta in frequenza di disturbo
- Metriche di stabilità ad anello aperto:frequenze di crossover a guadagno unitario e -180 gradi
Il modello del sistema servoidraulico aveva le seguenti caratteristiche:
- L'attuatore idraulico era un progetto "standard" utilizzato per anni per sviluppare strumenti analitici e di modellazione Simulink.
- Il carico utile era solo di massa, con la massa variata per ottenere frequenze della colonna d'olio (larghezze di banda) di 25, 50 e 100 Hz.
- La larghezza di banda della servovalvola era limitata a 2 x larghezza di banda del carico utile.
- La larghezza di banda di condizionamento del feedback è stata impostata su 10 x larghezza di banda del carico utile.
- La modalità di controllo era lo spostamento.
- L'algoritmo di controllo era Proportional-Integral-Derivative (PID) con ottimizzazione ottimizzata per ogni larghezza di banda del payload, frequenza di campionamento e latenza utilizzando un autotuner. I guadagni ottimizzati includevano: guadagno proporzionale sull'errore di spostamento; guadagno di stabilizzazione delta-p; frequenza di taglio passa-alto delta-p.
Per maggiori dettagli su questo modello servoidraulico, vedere Actuator Model.pdf , Actuator Transfer Functions.pdf e PID Transfer Functions.pdf.
Fedeltà del controllo (come funzione di frequenza di campionamento)
Per determinare l'effetto della frequenza di campionamento sulla fedeltà del controllo, il sistema è stato analizzato con frequenze di campionamento di controllo di 2 kHz, 5 kHz, 10 kHz e 20 kHz e larghezze di banda del sistema di 25 Hz, 50 Hz e 100 Hz. La latenza era il minimo possibile: 1.5 periodi di campionamento del controller. Nelle pagine seguenti sono riportati i confronti della risposta in frequenza ad anello chiuso, disturbo e ad anello aperto.
I grafici mostrano chiaramente che la maggior parte del vantaggio di una maggiore frequenza di campionamento si ottiene aumentando la frequenza di campionamento da 2 kHz a 5 kHz. Oltre a ciò, il miglioramento che è possibile ottenere è limitato.
Effetto su una frequenza di campionamento su un sistema a banda a 25 Hz
La risposta in frequenza ad anello chiuso è leggermente migliorata (più piatta) quando la frequenza di campionamento viene aumentata da 2 kHz a 5 kHz. Oltre a ciò, il miglioramento che è possibile ottenere è limitato:
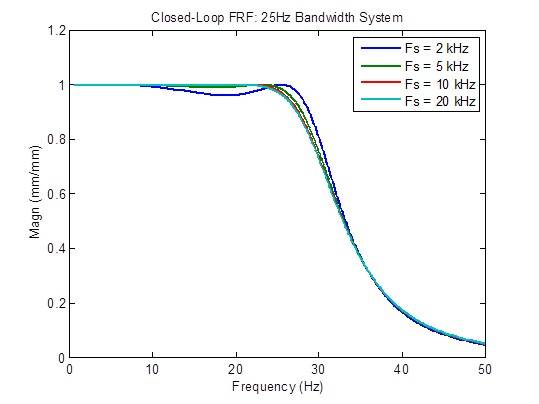
La risposta del disturbo è leggermente migliorata (più piatta) quando la frequenza di campionamento viene aumentata da 2 kHz a 5 kHz. Oltre a ciò, il miglioramento che è possibile ottenere è limitato:
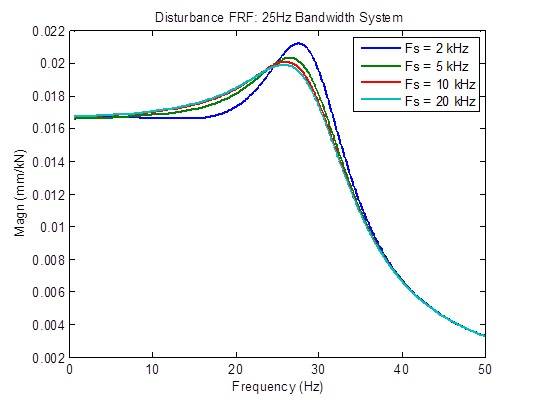
Quando la frequenza di campionamento viene aumentata da 2 kHz a 5 kHz, si verifica una leggera riduzione del picco della risposta in frequenza ad anello aperto. Oltre a ciò, il miglioramento che è possibile ottenere è limitato. Le metriche di stabilità (frequenze di crossover) sono per lo più invariate:
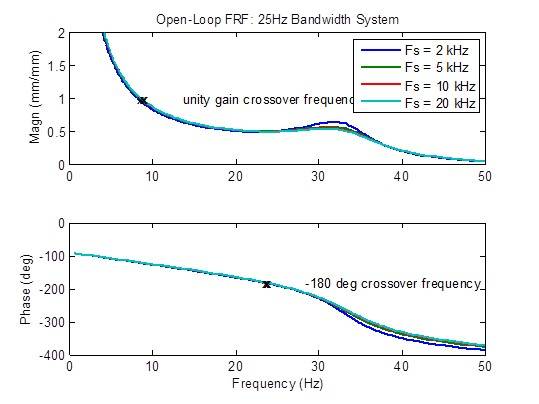
Effetto su una frequenza di campionamento su un sistema a banda a 50 Hz
La risposta in frequenza ad anello chiuso è leggermente migliorata (più piatta) quando la frequenza di campionamento viene aumentata da 2 kHz a 5 kHz. Oltre a ciò, il miglioramento che è possibile ottenere è limitato:
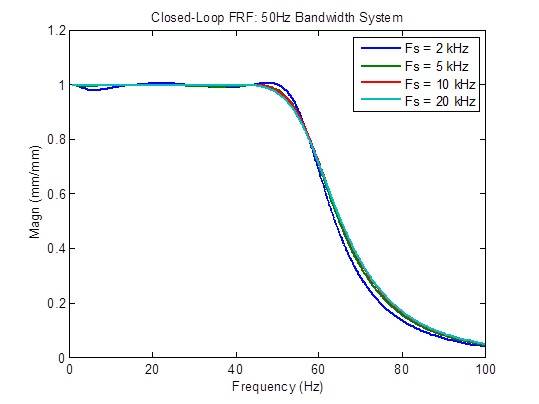
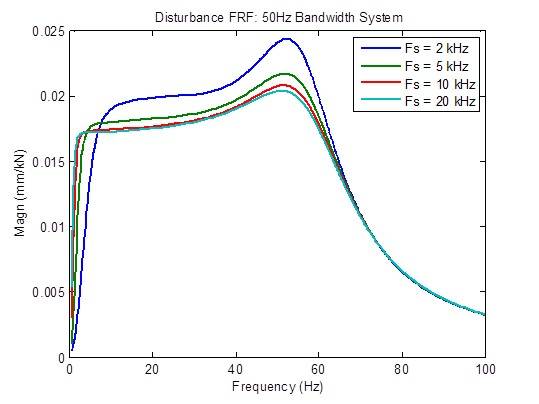
La risposta del disturbo è moderatamente migliorata (ridotta) quando la frequenza di campionamento viene aumentata da 2 kHz a 5 kHz e leggermente migliorata quando la frequenza di campionamento viene aumentata da 5 kHz e 10 kHz. Oltre a ciò, il miglioramento che è possibile ottenere è limitato:
Quando la frequenza di campionamento viene aumentata da 2 kHz a 5 kHz, si verifica una leggera riduzione del picco della risposta in frequenza ad anello aperto.Anche le metriche di stabilità (frequenze di crossover) sono leggermente migliorate (frequenza più alta). Oltre a ciò, il miglioramento che è possibile ottenere è limitato.
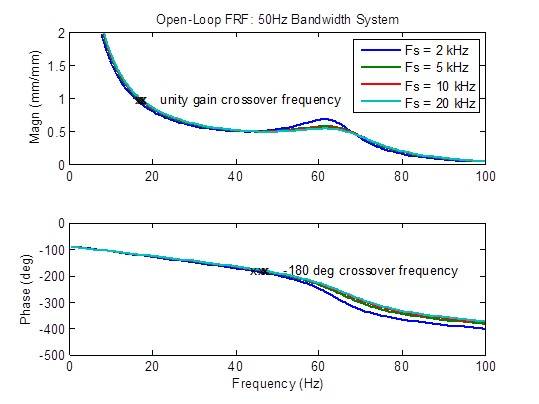
Effetto su una frequenza di campionamento su un sistema a banda a 100 Hz
La risposta in frequenza ad anello chiuso è significativamente migliorata (più piatta) quando la frequenza di campionamento viene aumentata da 2 kHz a 5 kHz. Oltre a ciò, il miglioramento che è possibile ottenere è limitato:
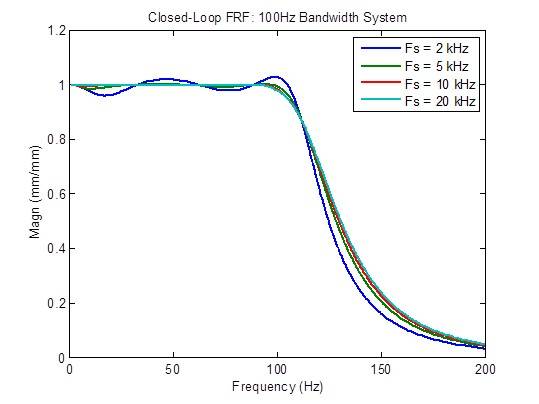
La risposta del disturbo è moderatamente migliorata (ridotta) quando la frequenza di campionamento viene aumentata da 2 kHz a 5 kHz e leggermente migliorata da 5 kHz e 10 kHz. Oltre a ciò, il miglioramento che è possibile ottenere è limitato.
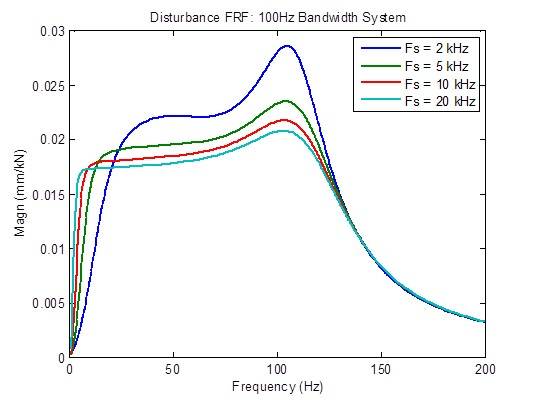
Quando la frequenza di campionamento viene aumentata da 2 kHz a 5 kHz, si verifica una riduzione moderata del picco della risposta in frequenza ad anello aperto.Anche le metriche di stabilità (frequenze di crossover) sono moderatamente migliorate (frequenza più alta).Oltre a ciò, il miglioramento che è possibile ottenere è limitato:
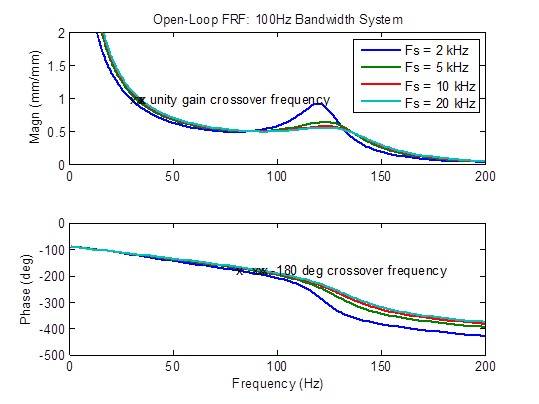
Fedeltà del controllo (come funzione di latenza)
L'aumento della frequenza di campionamento ad un certo punto sovraccaricherà un singolo processore in tempo reale, un problema che può essere risolto aggiungendo più processori e condividendo il carico computazionale tra di loro.
Tuttavia, la condivisione del carico aumenta la latenza, che è definita come il numero di campioni di ritardo tra la lettura dei feedback dei sensori e la scrittura dei comandi della servovalvola, secondo la formula
Latenza (campioni) = numero di processori + 0.5
La cifra 0,5 è il ritardo dovuto alla conversione da digitale ad analogico. La latenza minima possibile è 1,5 campioni, che si verifica quando è presente un solo processore. La latenza dovuta al numero di processori nasce dalla necessità di sincronizzare il passaggio dei dati di segnale da un processore al successivo.
Per determinare l'effetto della latenza sulla fedeltà del controllo, è stato analizzato un sistema con larghezza di banda di 100 Hz e frequenza di campionamento di 10 kHz con latenze di 1,5, 4 e 10 campioni. Nelle pagine seguenti sono riportati i confronti della risposta in frequenza ad anello chiuso, disturbo e ad anello aperto.
I grafici seguenti mostrano chiaramente che la fedeltà del controllo si riduce significativamente quando la latenza viene aumentata oltre il minimo di 1,5 campioni.Ciò dimostra che l'aggiunta di processori per ottenere una frequenza di campionamento elevata non è necessariamente una buona cosa e che potrebbe essere meglio utilizzare una frequenza di campionamento inferiore che sia alla portata di un singolo processore.
Nota: Il motivo per cui è stata scelta una frequenza di campionamento di 10 kHz e una latenza massima di 10 campioni per questa analisi è perché queste sono le specifiche di un controller offerto da un concorrente MTS.I grafici finali in questa sezione confrontano il controller di questo concorrente con un controller che ha la frequenza di campionamento ottimale di 5 kHz e la latenza minima di 1,5 campioni; il controller del concorrente è chiaramente inferiore.
Effetto di latenza su un sistema a banda a 100 Hz con una frequenza di campionamento a 10 kHz
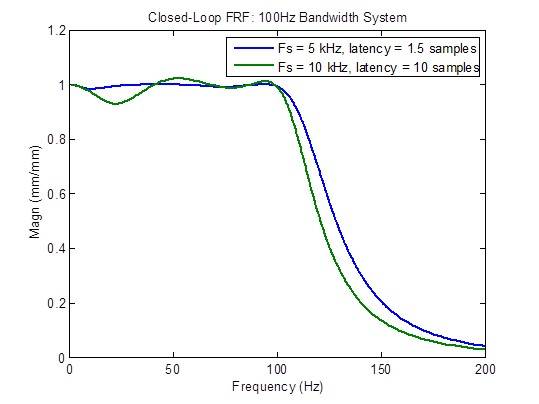
La risposta in frequenza ad anello chiuso degrada (diventa meno piatta) considerevolmente quando la latenza è maggiore del minimo di 1,5 campioni:
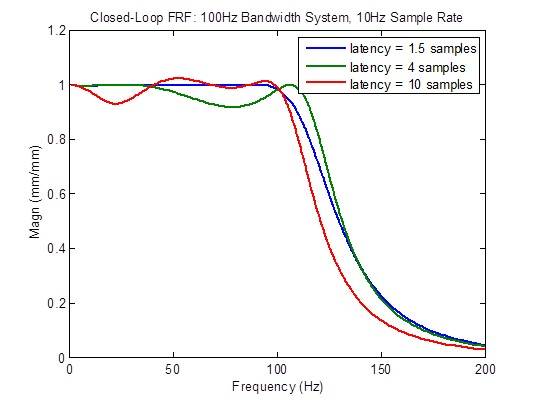
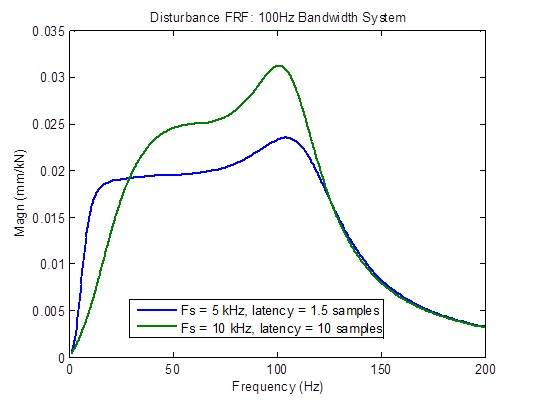
La risposta del disturbo degrada (diventa più alta) considerevolmente quando la latenza è maggiore del minimo di 1,5 campioni: Tuttavia, si verifica un miglioramento alle basse frequenze per ragioni al momento sconosciute:
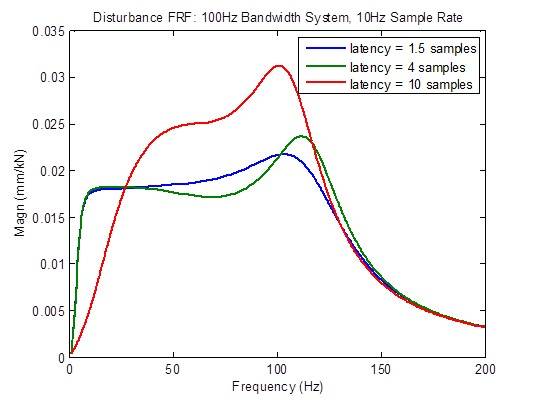
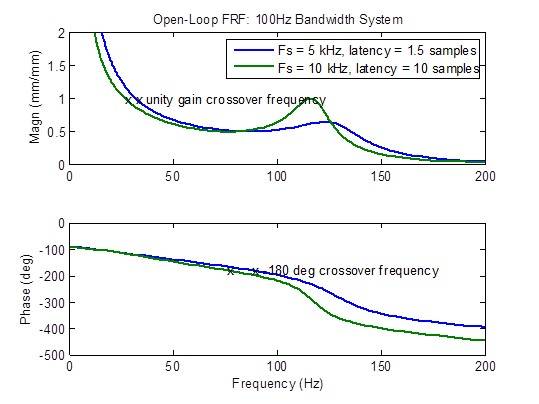
La risposta in frequenza ad anello aperto degrada (sviluppa picchi) considerevolmente quando la latenza è maggiore del minimo di 1,5 campioni. Le metriche di stabilità (frequenze di crossover) degradano (si verificano a frequenze più basse) considerevolmente:
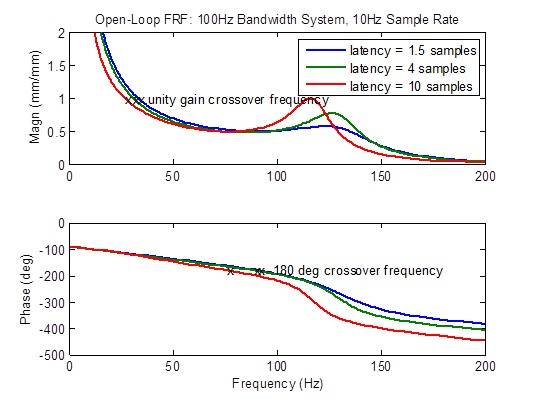
Confronto tra un sistema a banda a 100 Hz con una frequenza di campionamento a 10 kHz con alta latenza e una frequenza di campionamento a 5 kHz con latenza minima
Un rivale di MTS sostiene di avere un controller di frequenza di campionamento a 10kHz con latenza di 1 millisecondo (10 campioni @ 10 kHz). I grafici di frequenza seguenti mostrano chiaramente una risposta inferiore sotto ogni aspetto rispetto a una frequenza di campionamento di 5 kHz con latenza minima (1,5 campioni): larghezza di banda ridotta, risposta in frequenza ad anello chiuso non piatta, risposta ai disturbi più elevata e margini di stabilità degradati.
Effetti numerici
Effetti numerici dannosi come la quantizzazione del coefficiente e l'errore di arrotondamento peggiorano con l'aumento della frequenza di campionamento e si manifestano in diversi modi:
I processi integrativi hanno tassi di integrazione imprevedibili o possono bloccarsi: Esempi di tali processi includono generatori di funzioni di rampa e integratori di controller PID. Prendendo come esempio la generazione della rampa, la formula seguente genera un valore di rampa al tempo k aggiungendo un valore delta Δ = tasso di integrazione/frequenza di campionamento all'uscita precedente al tempo k - 1:
yk= ek-1 + Δ
| 1 kHz | 10 kHz | 100 kHz | |
| a1 = -1,991114 | a1 = -1,999111 | a1 = -1,999911 | |
| a2 = 0,991154 | a2 = 0,999112 | a2 = 0,999911 | |
Solo i coefficienti a1 e a2 sono di interesse, poiché sono quelli che determinano la stabilità e sono più suscettibili all'errore di arrotondamento e agli effetti di quantizzazione. Notare che all'aumentare della frequenza di campionamento, il numero di cifre che non sono 9 diminuisce. Ciò significa che ci sono molte meno cifre che determinano la risposta del filtro. Alla fine, con l'ulteriore aumento della frequenza di campionamento, il coefficiente a1 si avvicina a un valore di -2,0 e a2 si avvicina a un valore di 1,0. Ad un certo punto, la quantizzazione del coefficiente del filtro potrebbe portare a un filtro la cui risposta in frequenza è irregolare o addirittura instabile, in cui l'uscita oscilla con un valore elevato anche con ingresso zero.

