
Las personas que no están familiarizadas con los sistemas de control digital creen que cuanto mayor es la frecuencia de muestreo, mejor es la fidelidad del control.Es cierto que la fidelidad del control mejora al aumentar la frecuencia de muestreo, pero solo hasta cierto punto. Más allá de ese punto, el control es esencialmente analógico y no se producen más mejoras.Si la frecuencia de muestreo aumenta aún más, la fidelidad del control se degrada debido a efectos numéricos perjudiciales como la cuantificación del coeficiente y el error de redondeo.
Como se demostrará en este informe, la regla general para los sistemas servohidráulicos es que la frecuencia de muestreo óptima sea cincuenta veces el ancho de banda del sistema, definido como la frecuencia natural de la columna de aceite (o cualquier otro modo dinámico dominante). El ancho de banda de la mayoría de los sistemas servohidráulicos MTS es de 100 Hz o menos, por lo que basta con una frecuencia de muestreo de 100 x 50 = 5 kHz. Más allá de esta frecuencia de muestreo, hay poca o ninguna mejora en la fidelidad del control.
La frecuencia de muestreo a la que se degrada el control debido a los efectos numéricos es difícil de determinar, ya que depende de muchos factores, como la precisión numérica, la amplitud y el ancho de banda de la señal, las frecuencias de ruptura de los filtros digitales, etc. Solo se puede encontrar mediante pruebas exhaustivos (es decir, costosas).
Aumentar la frecuencia de muestreo más allá del punto óptimo aumenta el costo del hardware en tiempo real. También hay un costo de oportunidad perdida: Como gran parte del ancho de banda del procesador en tiempo real se desperdicia en cálculos que no mejoran la fidelidad del control, queda poco ancho de banda para los algoritmos de control avanzados que sí mejoran la fidelidad, como el control inverso adaptativo (AIC).
Este informe limita la discusión al control de la frecuencia de muestreo. Hay otras frecuencias de muestreo en un controlador, como la frecuencia de muestreo de adquisición de datos. Puede haber buenas razones para tener una frecuencia de muestreo de adquisición de datos mucho más alta que la del controlador de circuito cerrado.
Se consideran los siguientes temas:
- Controle la fidelidad en función de la frecuencia de muestreo
- Fidelidad de control en función de la latencia (definida como el número de muestras de retardo entre la lectura de las retroalimentaciones de los sensores y la escritura de los comandos de las servoválvulas)
- Efectos numéricos
Las conclusiones a las que se llegó en este informe se resumen a continuación:
- La frecuencia de muestreo de control óptima para la mayoría de los sistemas servohidráulicos MTS es de 5 kHz.Las frecuencias de muestreo más altas producen poco o ningún beneficio.
- La obtención de frecuencias de muestreo más altas compartiendo la carga entre varios procesadores en tiempo real aumenta la latencia, lo que degrada significativamente la fidelidad del control.
La fidelidad del control se analizó utilizando un análisis de respuesta de frecuencia de un sistema servohidráulico típico de varios anchos de banda, frecuencias de muestreo y latencias, y comparando:
- Respuesta de frecuencia de circuito cerrado
- Respuesta de frecuencia de perturbación
- Medidas de estabilidad de circuito abierto:frecuencias de cruce de ganancia unitaria y -180 grados
El modelo del sistema servohidráulico tenía las siguientes características:
- El actuador hidráulico fue un diseño "estándar" utilizado durante años para desarrollar herramientas analíticas y de modelado de Simulink.
- La carga útil era solo de masa, con la masa variada para obtener frecuencias de columna de aceite (anchos de banda) de 25, 50 y 100 Hz.
- El ancho de banda de la servoválvula se limitó a 2 x ancho de banda de carga útil.
- El ancho de banda de acondicionamiento de retroalimentación se estableció en 10 x ancho de banda de carga útil.
- El modo de control fue el desplazamiento.
- El algoritmo de control fue proporcional-integral-derivado (PID) con ajuste optimizado para cada ancho de banda de carga útil, frecuencia de muestreo y latencia utilizando un autoajuste. Las ganancias optimizadas incluyen: ganancia proporcional al error de desplazamiento; ganancia de estabilización delta-p; frecuencia de corte de paso alto delta-p.
Para obtener más detalles sobre este modelo servohidráulico, consulte Modelo del actuator Model.pdf, Funciones de transferencia del actuator.pdf y Funciones de transferencia PID.pdf.
Fidelidad de control (en función de la frecuencia de muestreo)
. Para determinar el efecto de la frecuencia de muestreo en la fidelidad del control, el sistema se analizó con frecuencias de muestreo de control de 2 kHz, 5 kHz, 10 kHz y 20 kHz, y con anchos de banda del sistema de 25 Hz, 50 Hz y 100 Hz. La latencia fue la mínima possible: 1,5 períodos de muestreo del controlador. En las siguientes páginas se comparan las respuestas de frecuencia en circuito cerrado, perturbado y en circuito abierto.
Los gráficos muestran claramente que la mayor parte del beneficio del aumento de la frecuencia de muestreo se obtiene al aumentar la frecuencia de muestreo de 2 kHz a 5 kHz. Más allá de eso, hay pocas mejoras que se pueden obtener.
Efecto de la frecuencia de muestreo en un sistema de ancho de banda de 25 Hz.
La respuesta de frecuencia de circuito cerrado mejora algo (más plana) cuando la frecuencia de muestreo aumenta de 2 kHz a 5 kHz. Más allá de eso, hay pocas mejoras:
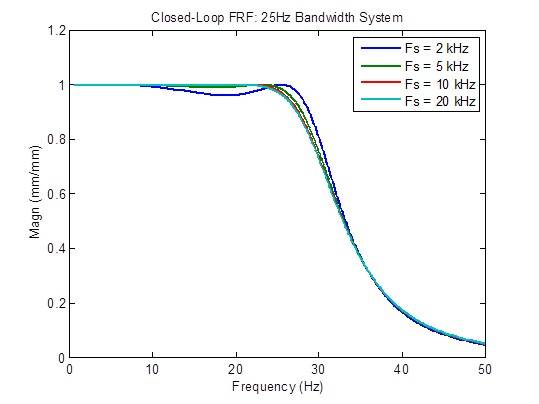
La respuesta a las perturbaciones mejora un poco (se reduce) cuando se aumenta la frecuencia de muestreo de 2 kHz a 5 kHz. Más allá de eso, hay pocas mejoras:
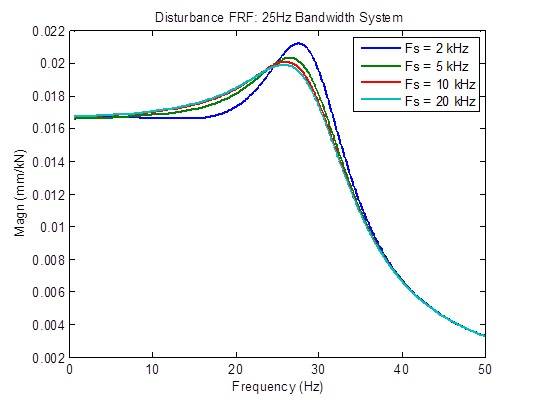
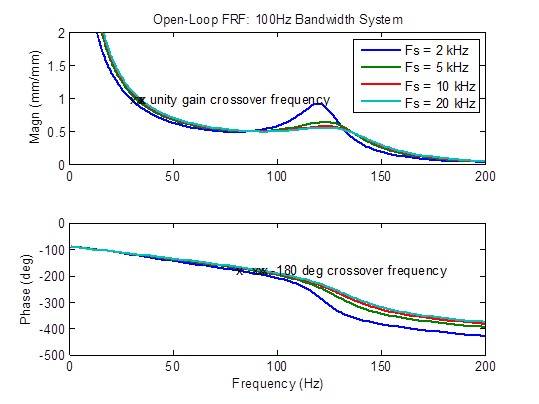
Hay una ligera reducción en el pico de la respuesta de frecuencia de circuito abierto cuando la frecuencia de muestreo aumenta de 2 kHz a 5 kHz. Más allá de eso, hay pocas mejoras. Las medidas de estabilidad (frecuencias de cruce) no cambian en su mayor parte:
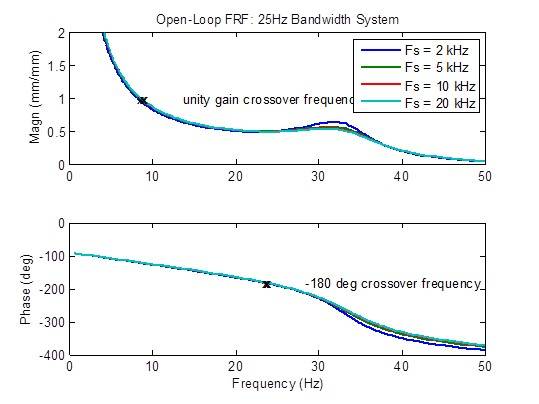
Efecto de la frecuencia de muestreo en un sistema
. La respuesta en frecuencia del bucle cerrado mejora ligeramente (es más plana) cuando la frecuencia de muestreo aumenta de 2 kHz a 5 kHz. Más allá de eso, hay pocas mejoras:
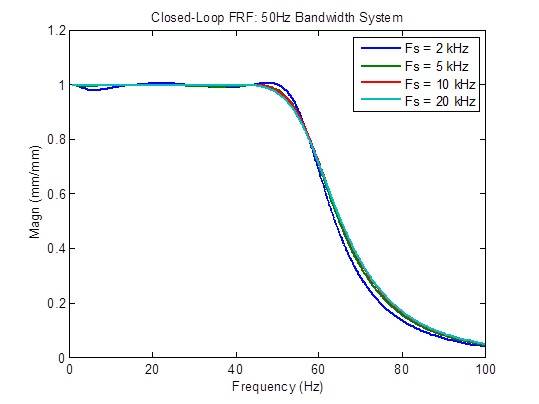
La respuesta a las perturbaciones mejora moderadamente (se reduce) cuando se aumenta la frecuencia de muestreo de 2 kHz a 5 kHz, y mejora algo cuando se aumenta la frecuencia de muestreo de 5 kHz a 10 kHz. Más allá de eso, hay pocas mejoras:
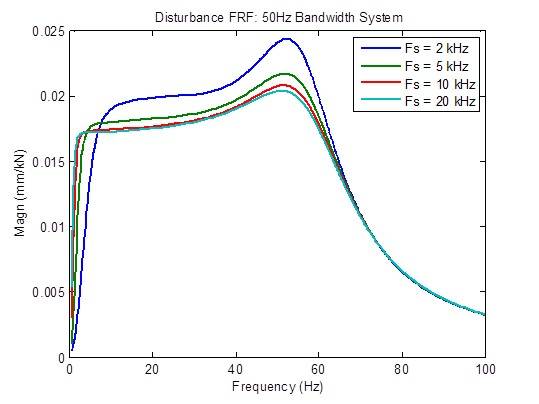
Hay una ligera reducción en el pico de la respuesta de frecuencia de circuito abierto cuando la frecuencia de muestreo aumenta de 2 kHz a 5 kHz. Las medidas de estabilidad (frecuencias de cruce) también mejoran un poco (frecuencia más alta). Más allá de eso, hay pocas mejoras.
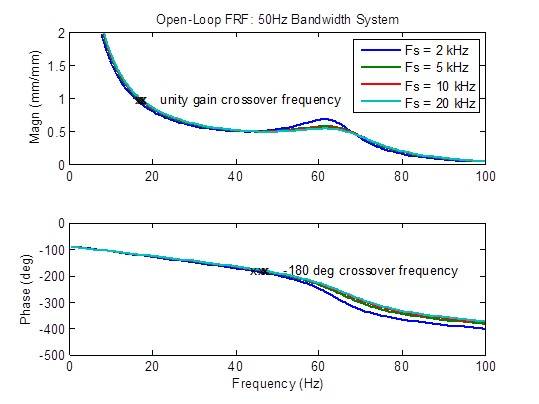
Efecto de la frecuencia de muestreo en un sistema de ancho de banda de 50 Hz.
La respuesta en frecuencia del bucle cerrado mejora ligeramente (es más plana) cuando la frecuencia de muestreo aumenta de 2 kHz a 5 kHz. Más allá de eso, hay pocas mejoras:
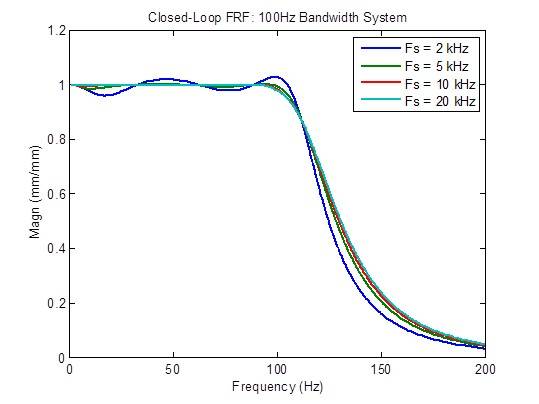
La respuesta a las perturbaciones mejora moderadamente (se reduce) cuando se aumenta la frecuencia de muestreo de 2 kHz a 5 kHz, y mejora algo de 5 kHz a 10 kHz. Más allá de eso, hay pocas mejoras.
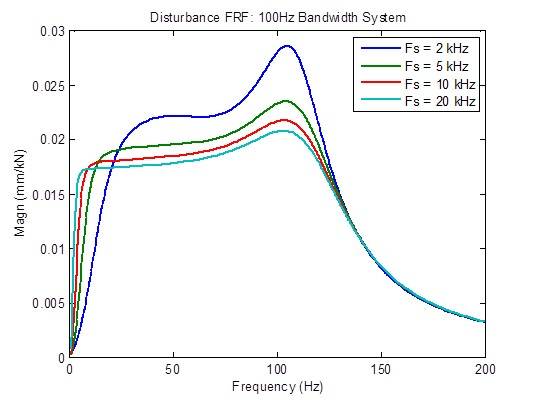
Hay una reducción moderada en el pico de la respuesta de frecuencia de circuito abierto cuando la frecuencia de muestreo aumenta de 2 kHz a 5 kHz. Las métricas de estabilidad (frecuencias de cruce) también mejoran ligeramente (mayor frecuencia).Más allá de eso, hay pocas mejoras:
Fidelidad de control (en función de la latencia)
. Al aumentar la frecuencia de muestreo, en algún momento se sobrecargará un solo procesador en tiempo real, un problema que se puede resolver agregando más procesadores y compartiendo la carga computacional entre ellos.
Sin embargo, la carga compartida aumenta la latencia, que se define como el número de muestras de retraso entre la lectura de las retroalimentaciones del sensor y la escritura de los comandos de la servoválvula, de acuerdo con la fórmula.
Latencia (muestras) = número de procesadores + 0.5
La cifra de 0,5 es un retraso debido a la conversión de digital a analógico. La latencia mínima posible es de 1,5 muestras, que se produce cuando solo hay un procesador presente. La latencia derivada del número de procesadores se debe a la necesidad de sincronizar el paso de los datos de la señal de un procesador al siguiente.
Para determinar el efecto de la latencia en la fidelidad del control, se analizó un sistema con un ancho de banda de 100 Hz y una frecuencia de muestreo de 10 kHz con latencias de 1,5, 4 y 10 muestras. En las siguientes páginas se comparan las respuestas de frecuencia en circuito cerrado, perturbado y en circuito abierto.
Los siguientes gráficos muestran claramente que la fidelidad del control se degrada significativamente cuando la latencia aumenta más allá del mínimo de 1,5 muestras.Esto demuestra que agregar procesadores para lograr una alta frecuencia de muestreo no es necesariamente algo bueno y que podría ser mejor utilizar una frecuencia de muestreo menor que esté dentro de la capacidad de un solo procesador.
Nota La razón por la que se eligió una frecuencia de muestreo de 10 kHz y una latencia máxima de 10 muestras para este análisis es que estas son las especificaciones de un controlador de la competencia de MTS.Los gráficos finales de esta sección comparan el controlador de este competidor con un controlador que tiene la frecuencia de muestreo óptima de 5 kHz y la latencia mínima de 1,5 muestras; el controlador del competidor es claramente inferior.
Efecto de la latencia en un sistema de ancho de banda de 100 Hz con una frecuencia de muestreo de 10 kHz.
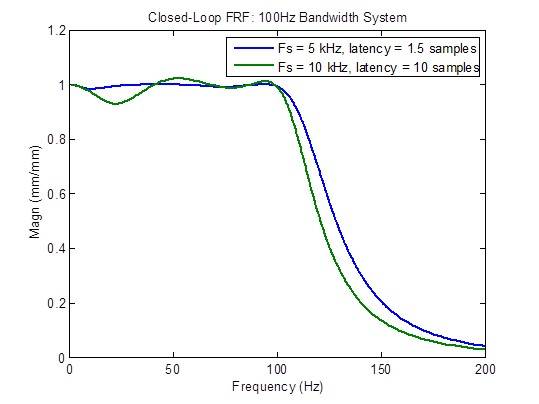
La respuesta de la frecuencia en circuito cerrado se degrada (se vuelve menos plana) considerablemente cuando la latencia es mayor que el mínimo de 1,5 muestras:
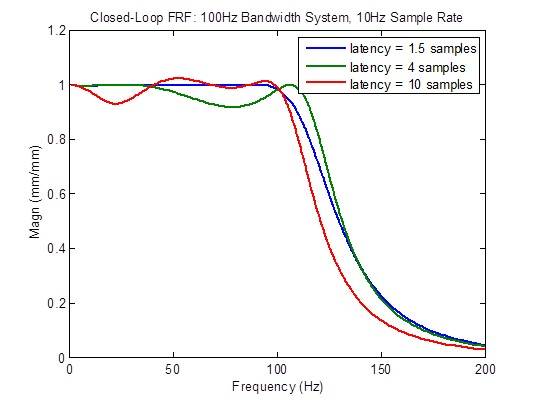
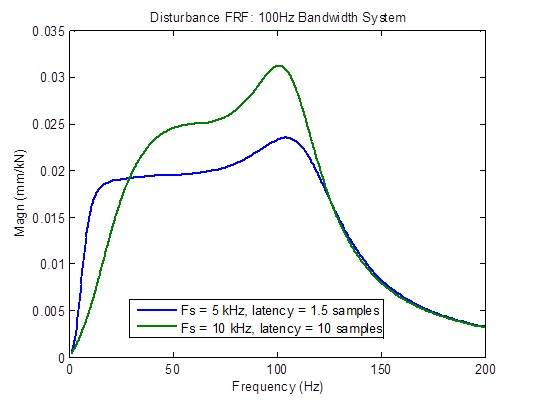
La respuesta a las perturbaciones se degrada considerablemente (se vuelve más alta) cuando la latencia es mayor que el mínimo de 1,5 muestras. Sin embargo, hay una mejora en las frecuencias bajas debido a razones que se desconocen en este momento:
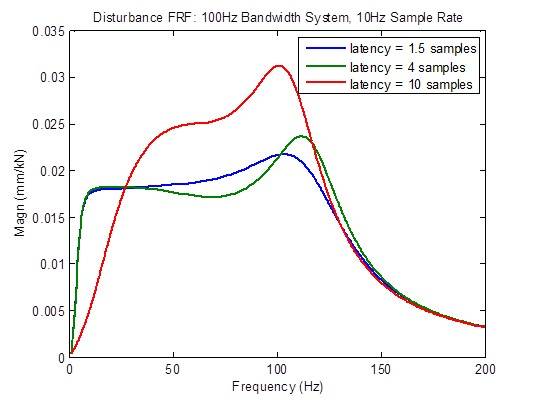
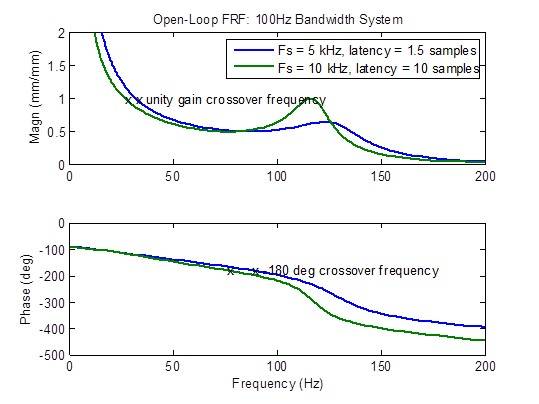
La respuesta de frecuencia en circuito abierto se degrada (desarrolla picos) considerablemente cuando la latencia es mayor que el mínimo de 1,5 muestras. Las medidas de estabilidad (frecuencias de cruce) se degradan (ocurren a frecuencias más bajas) considerablemente:
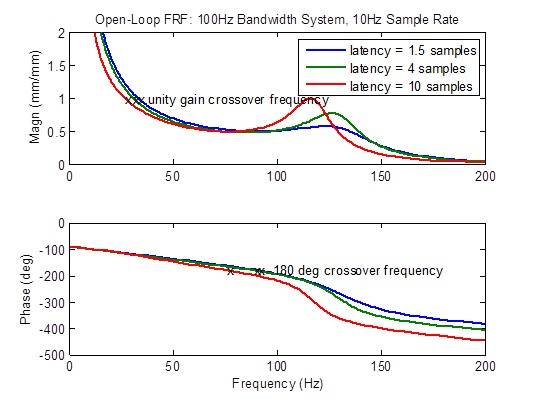
Comparación de un sistema de ancho de banda de 100 Hz con una tasa de muestreo de 10 kHz con alta latencia frente a una tasa de muestreo de 5 kHz con una latencia mínima.
Un competidor de MTS afirma tener un controlador de tasa de muestreo de 10 kHz con una latencia de 1 milisegundo (10 muestras a 10 kHz). Los gráficos de frecuencia a continuación muestran claramente una respuesta inferior en todos los aspectos en comparación con una frecuencia de muestreo de 5 kHz con latencia mínima (1,5 muestras): ancho de banda reducido, respuesta de frecuencia de circuito cerrado no plano, mayor respuesta a perturbaciones y márgenes de estabilidad degradados.
Efectos numéricos.
Los efectos numéricos perjudiciales, como la cuantificación de los coeficientes y el error de redondeo, empeoran al aumentar la frecuencia de muestreo y se manifiestan de varias maneras:
Los procesos de integración tienen tasas de integración impredecibles o pueden atascarse: Algunos ejemplos de estos procesos son los generadores de funciones de rampa y los integradores de controladores PID. Tomando la generación de rampa como ejemplo, la siguiente fórmula genera un valor de rampa en el momento k al agregar un valor delta Δ = tasa de integración/frecuencia de muestreo a la salida anterior en el momento k - 1:
yk = yk-1 + Δ
| 1 kHz | 10 kHz | 100 kHz | |
| a1 = -1,991114 | a1 = -1,999111 | a1 = -1,999911 | |
| a2 = 0,991154 | a2 = 0,999112 | a2 = 0,999911 | |
Solo son de interés los coeficientes a1 y a2 , porque son los que determinan la estabilidad y son los más susceptibles al error de redondeo y a los efectos de cuantificación. Tenga en cuenta que a medida que aumenta la frecuencia de muestreo, disminuye el número de dígitos que no son 9. Esto significa que hay muchos menos dígitos que determinan la respuesta del filtro. Finalmente, a medida que la frecuencia de muestreo se incrementa más, el coeficiente a1 se acerca a un valor de -2,0 y a2 se acerca a un valor de 1,0. En algún momento, la cuantificación del coeficiente del filtro podría dar lugar a un filtro cuya respuesta en frecuencia es errática o incluso inestable, donde la salida oscila con un gran valor incluso con una entrada cero.

