
Menschen, die mit digitalen Regelungssystemen nicht vertraut sind, glauben, dass die Regelungstreue umso besser ist, je höher die Abtastrate ist. Es stimmt, dass sich die Regeltreue mit steigender Abtastrate verbessert, aber nur bis zu einem bestimmten Punkt. Jenseits dieses Punktes ist die Steuerung im Wesentlichen analog, und es tritt keine weitere Verbesserung ein.Wenn die Abtastrate noch weiter erhöht wird, verschlechtert sich die Regeltreue aufgrund nachteiliger numerischer Effekte wie Koeffizientenquantisierung und Rundungsfehler sogar.
Wie in diesem Bericht gezeigt wird, gilt als Faustregel für servohydraulische Systeme, dass die optimale Abtastrate das Fünfzigfache der Systembandbreite beträgt, definiert als die Eigenfrequenz der Ölsäule (oder eine andere dominante dynamische Mode). Die Bandbreite der meisten MTS-Servohydrauliksysteme beträgt 100 Hz oder weniger, sodass eine Abtastrate von 100 x 50 = 5 kHz ausreichend ist. Jenseits dieser Abtastrate gibt es nur eine geringe oder gar keine Verbesserung der Regelungstreue.
Die Abtastrate, bei der die Regelung aufgrund von numerischen Effekten nachlässt, ist schwer zu bestimmen, da sie von vielen Faktoren abhängt, z. B. von der numerischen Präzision, der Signalamplitude und -bandbreite, den Unterbrechungsfrequenzen der digitalen Filter usw. Sie kann nur durch ausführliche (d. h. teure) Tests gefunden werden.
Eine Erhöhung der Abtastrate über den optimalen Punkt hinaus erhöht die Kosten für die Echtzeit-Hardware. Außerdem gibt es Kosten für verpasste Möglichkeiten: Da ein Großteil der Echtzeit-Prozessorbandbreite für Berechnungen verschwendet wird, die die Regelungstreue nicht verbessern, bleibt nur wenig Bandbreite für fortschrittliche Regelungsalgorithmen übrig, die die Regelungstreue verbessern, wie z. B. die adaptive inverse Regelung (AIC).
Dieser Bericht beschränkt die Diskussion auf die Regelung der Abtastrate. In einem Regler gibt es weitere Abtastraten, wie z. B. die Abtastrate der Datenerfassung. Es kann gute Gründe geben, eine Abtastrate der Datenerfassung zu haben, die viel höher ist als die des Reglers.
Die folgenden Themen werden berücksichtigt:
- Regelungstreue in Abhängigkeit von der Abtastrate
- Regelungstreue in Abhängigkeit von der Latenz (definiert als die Anzahl der Prüflinge der Verzögerung zwischen dem Lesen der Sensorrückmeldungen und dem Schreiben der Servoventilbefehle)
- Numerische Effekte
Die in diesem Bericht getroffenen Feststellungen sind hier zusammengefasst:
- Die optimale Regelabtastrate für die meisten servohydraulischen Systeme von MTS beträgt 5 kHz.Höhere Abtastraten bringen wenig bis keinen Nutzen.
- Die Erzielung höherer Abtastraten durch Lastverteilung auf mehrere Echtzeitprozessoren erhöht die Latenz, was die Regelungstreue erheblich verschlechtert.
Die Regelungstreue wurde mittels Frequenzganganalyse eines typischen servohydraulischen Systems mit verschiedenen Bandbreiten, Abtastraten und Latenzen analysiert und verglichen:
- Frequenzgang des geschlossenen Regelungskreises
- Frequenzgang der Störung
- Kennzahlen zur Steuerstabilität:Trennfrequenzen für einheitlichen Pegel und -180 Grad
Das Modell des servohydraulischen Systems hatte die folgenden Eigenschaften:
- Der hydraulische Aktuator war ein Standarddesign, das jahrelang für die Entwicklung von Analyse- und Simulink-Modellierungswerkzeugen verwendet wurde.
- Die Nutzlast war nur Masse, wobei die Masse variiert wurde, um Ölsäulenfrequenzen (Bandbreiten) von 25, 50 und 100 Hz zu erhalten.
- Die Servoventil-Bandbreite wurde auf 2 x Nutzlastbandbreite begrenzt.
- Die Bandbreite der Rückkopplungsaufbereitung wurde auf 10 x Nutzlastbandbreite eingestellt.
- Die Regelart war Verschiebung.
- Der Regelungsalgorithmus war Proportional-Integral-Derivativ (PID) mit einer für jede Nutzdatenbandbreite, Abtastrate und Latenz optimierten Abstimmung unter Verwendung eines Autotuners. Optimierte Verstärkung inklusive: Proportionalverstärkung auf den Verschiebungsfehler; Delta-P-Stabilisierungsverstärkung; Delta-P-Hochpass-Einschaltfrequenz.
Weitere Details zu diesem servohydraulischen Modell finden Sie unter Actuator Model.pdf , Actuator Transfer Functions.pdf und PID Transfer Functions.pdf.
Regelungstreue (in Abhängigkeit von der Abtastrate)
Um die Auswirkung der Abtastrate auf die Regeltreue zu bestimmen, wurde das System mit Regelabtastraten von 2 kHz, 5 kHz, 10 kHz und 20 kHz und Systembandbreiten von 25 Hz, 50 Hz und 100 Hz analysiert. Die Latenz war die minimal mögliche: 1,5 Reglerabtastperioden. Vergleiche des Frequenzgangs bei geschlossenem Regelkreis, bei Störung und bei offenem Regelkreis finden Sie auf den folgenden Seiten.
Die Diagramme zeigen deutlich, dass der größte Teil des Vorteils der erhöhten Abtastrate durch die Erhöhung der Abtastrate von 2 kHz auf 5 kHz erzielt wird. Darüber hinaus sind kaum Verbesserungen zu erzielen.
Auswirkung der Abtastrate auf ein System mit einer Bandbreite von 25 Hz
Der Frequenzgang des geschlossenen Regelkreises wird etwas verbessert (flacher), wenn die Abtastrate von 2 kHz auf 5 kHz erhöht wird. Darüber hinaus sind kaum Verbesserungen zu erzielen:
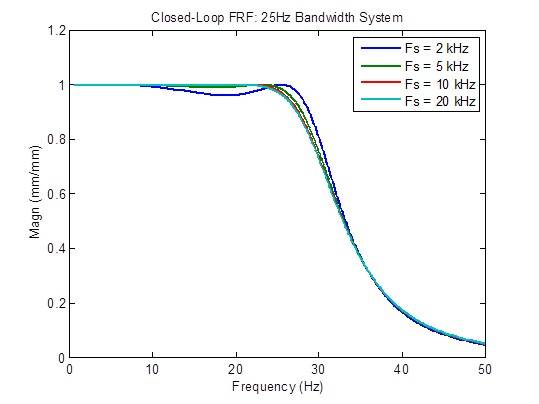
Die Reaktion auf Störungen wird etwas verbessert (flacher), wenn die Abtastrate von 2 kHz auf 5 kHz erhöht wird. Darüber hinaus sind kaum Verbesserungen zu erzielen:
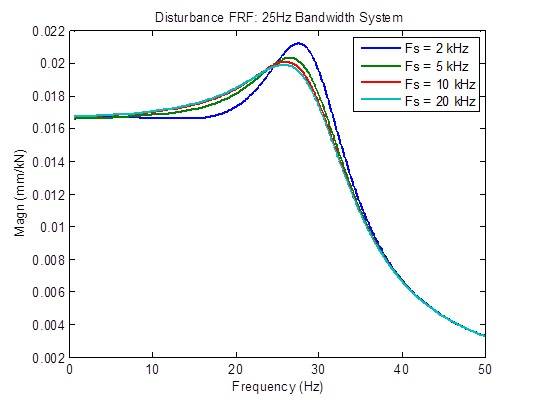
Es gibt eine leichte Verringerung des Spitzenwerts der Steuerfrequenzreaktion, wenn die Abtastrate von 2 kHz auf 5 kHz erhöht wird. Darüber hinaus sind kaum Verbesserungen zu erzielen. Die Stabilitätskennzahlen (Überschneidungsfrequenzen) sind weitgehend unverändert:
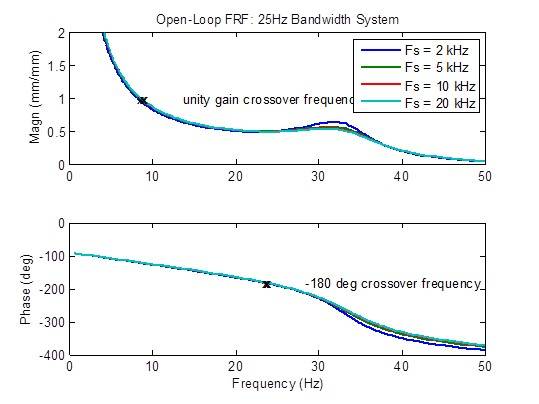
Auswirkung der Abtastrate auf ein System mit einer Bandbreite von 50 Hz
Der Frequenzgang des geschlossenen Regelkreises wird etwas verbessert (flacher), wenn die Abtastrate von 2 kHz auf 5 kHz erhöht wird. Darüber hinaus sind kaum Verbesserungen zu erzielen:
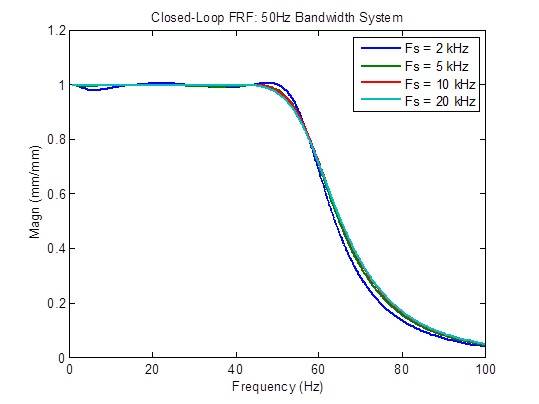
Die Reaktion auf Störungen wird etwas verbessert (verringert), wenn die Abtastrate von 2 kHz auf 5 kHz erhöht wird, und etwas verbessert, wenn die Abtastrate von 5 kHz auf 10 kHz erhöht wird. Darüber hinaus sind kaum Verbesserungen zu erzielen:
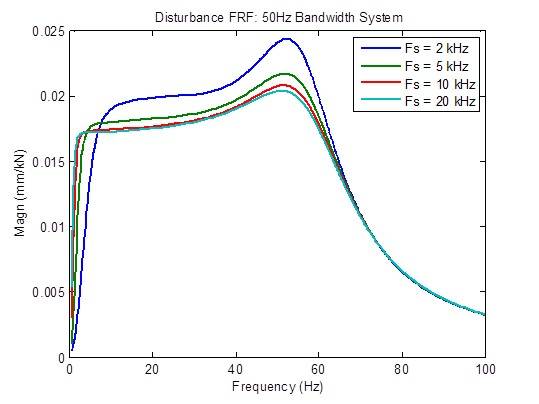
Es gibt eine leichte Verringerung des Spitzenwerts der Steuerfrequenzreaktion, wenn die Abtastrate von 2 kHz auf 5 kHz erhöht wird. Die Stabilitätskennzahlen (Übergangsfrequenzen) sind ebenfalls etwas verbessert (höhere Frequenz).Darüber hinaus sind kaum Verbesserungen zu erzielen:
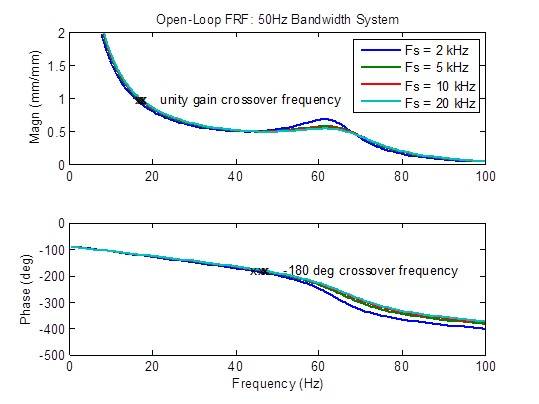
Auswirkung der Abtastrate auf ein System mit einer Bandbreite von 100 Hz
Der Frequenzgang des geschlossenen Regelkreises wird etwas verbessert (flacher), wenn die Abtastrate von 2 kHz auf 5 kHz erhöht wird. Darüber hinaus sind kaum Verbesserungen zu erzielen:
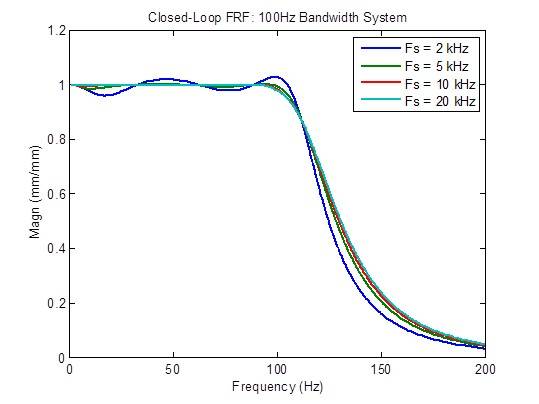
Die Reaktion auf Störungen wird etwas verbessert (verringert), wenn die Abtastrate von 2 kHz auf 5 kHz erhöht wird, und etwas von 5 kHz auf 10 kHz verbessert.Darüber hinaus sind kaum Verbesserungen zu erzielen:
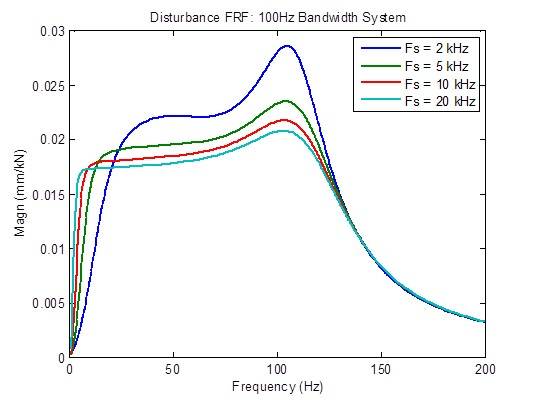
Es gibt eine mittlere Verringerung des Spitzenwerts der Steuerfrequenzreaktion, wenn die Abtastrate von 2 kHz auf 5 kHz erhöht wird.Die Stabilitätskennzahlen (Übergangsfrequenzen) sind ebenfalls etwas verbessert (höhere Frequenz).Darüber hinaus sind kaum Verbesserungen zu erzielen:
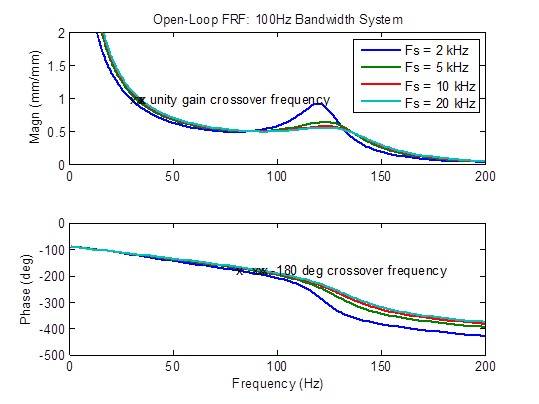
Regelungstreue (in Abhängigkeit von der Latenz)
Eine Erhöhung der Abtastrate überlastet irgendwann einen einzelnen Echtzeitprozessor, ein Problem, das durch Hinzufügen weiterer Prozessoren und Aufteilung der Rechenlast auf diese gelöst werden kann.
Die Lastverteilung erhöht jedoch die Latenz, die als Anzahl der Samples der Verzögerung zwischen dem Lesen von Sensorrückmeldungen und dem Schreiben von Servoventilbefehlen definiert ist, gemäß der Formel
Latenz (Prüflinge) = Anzahl der Prozessoren + 0.5
Der Wert 0,5 ist die Verzögerung durch die Digital-Analog-Wandlung. Die minimal mögliche Latenzzeit beträgt 1,5 Prüflinge, die auftritt, wenn nur ein Prozessor vorhanden ist. Die Latenz durch die Anzahl der Prozessoren ergibt sich aus der Notwendigkeit, den Durchlauf der Signaldaten von einem Prozessor zum nächsten zu synchronisieren.
Um die Auswirkung der Latenz auf die Regelungstreue zu bestimmen, wurde ein System mit 100 Hz Bandbreite und einer Abtastrate von 10 kHz mit Latenzen von 1,5, 4 und 10 Abtastungen analysiert. Vergleiche des Frequenzgangs bei geschlossenem Regelkreis, bei Störung und bei offenem Regelkreis finden Sie auf den folgenden Seiten.
Die folgenden Diagramme zeigen deutlich, dass sich die Regelungstreue deutlich verschlechtert, wenn die Latenz über das Minimum von 1,5 Prüflingen hinaus erhöht wird.Dies zeigt, dass das Hinzufügen von Prozessoren, um eine hohe Abtastrate zu erreichen, nicht unbedingt eine gute Sache ist, und dass es besser sein könnte, eine niedrigere Abtastrate zu verwenden, die innerhalb der Möglichkeiten eines einzelnen Prozessors liegt.
Hinweis: Der Grund, warum für diese Analyse eine Abtastrate von 10 kHz und eine maximale Latenz von 10 Prüflingen gewählt wurde, ist, dass dies die Spezifikationen eines Reglers sind, der von einem MTS-Wettbewerber angeboten wird.Die letzten Diagramme in diesem Abschnitt vergleichen den Regler dieses Wettbewerbers mit einem Regler, der die optimale Abtastrate von 5 kHz und die minimale Latenz von 1,5 Prüflingen hat; der Regler des Wettbewerbers ist deutlich unterlegen.
Auswirkung der Latenz auf ein System mit einer Bandbreite von 100 Hz und einer Abtastrate von 10 kHz
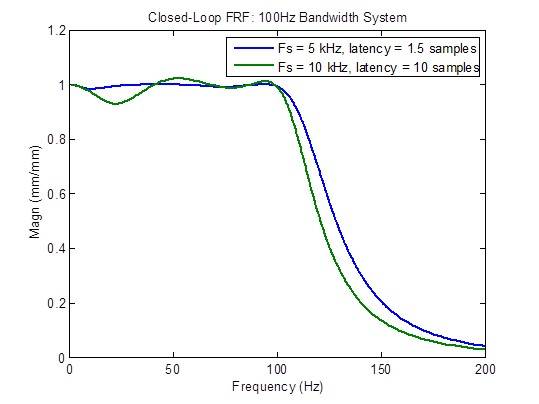
Der Frequenzgang des Regelkreises verschlechtert sich erheblich (wird weniger flach), wenn die Latenzzeit größer als das Minimum von 1,5 Prüflingen ist:
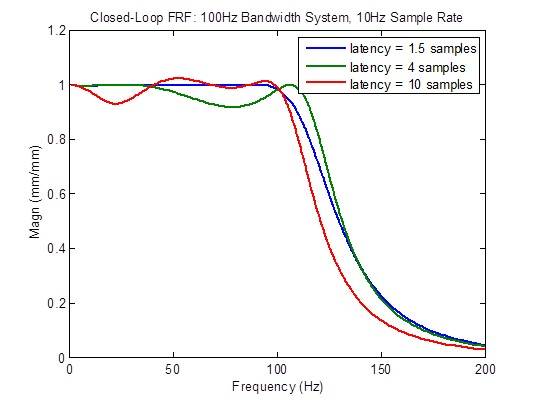
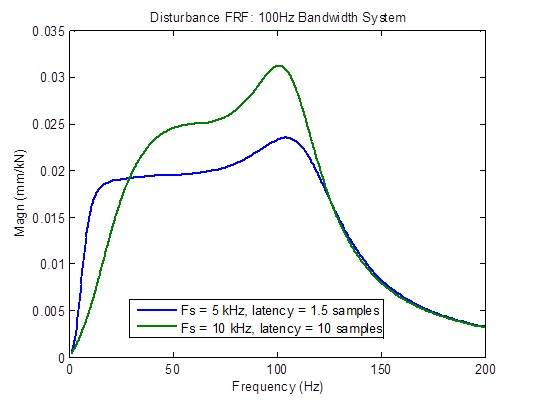
Die Störungsreaktion verschlechtert sich erheblich (wird höher), wenn die Latenzzeit größer als das Minimum von 1,5 Prüflingen ist. Es gibt jedoch eine Verbesserung bei niedrigen Frequenzen aus Gründen, die zu diesem Zeitpunkt noch nicht bekannt sind:
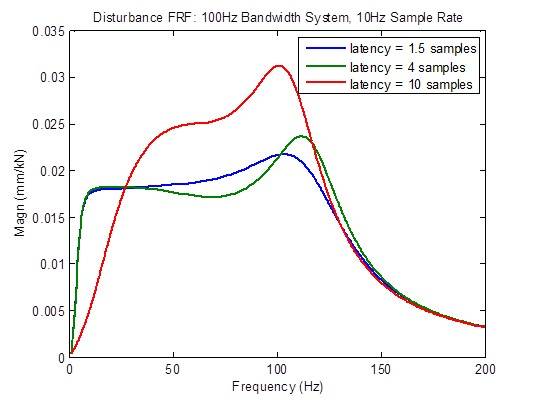
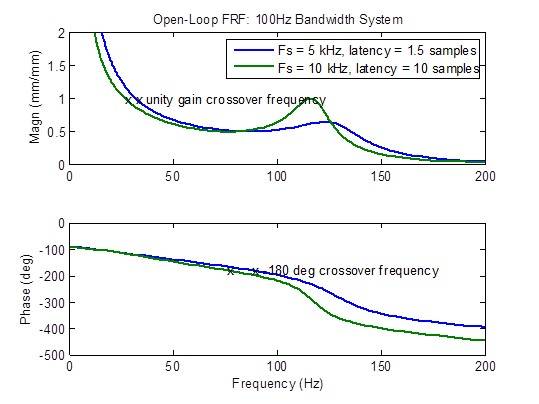
Der Frequenzgang des Steuerkreises verschlechtert sich erheblich (bildet Spitzen), wenn die Latenzzeit größer als das Minimum von 1,5 Prüflingen ist. Die Stabilitätszahlen (Übergangsfrequenzen) verschlechtern sich erheblich (treten bei niedrigeren Frequenzen auf):
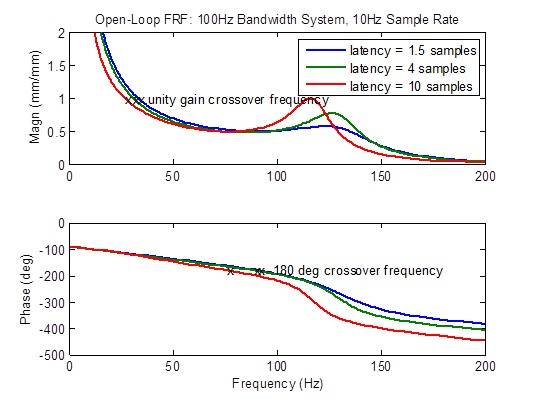
Vergleich eines Systems mit 100 Hz Bandbreite und einer Abtastrate von 10 kHz mit hoher Latenz gegenüber einer Abtastrate von 5 kHz mit minimaler Latenz
Ein MTS-Wettbewerber behauptet, einen Regler mit einer Abtastrate von 10 kHz mit einer Latenz von 1 Millisekunde zu haben (10 Prüflinge bei 10 kHz). Die Frequenzkurven unten zeigen deutlich den in jeder Hinsicht schlechteren Frequenzgang im Vergleich zu einer Abtastrate von 5 kHz mit minimaler Latenz (1,5 Prüflinge): reduzierte Bandbreite, nicht flacher Frequenzgang des Regelkreises, höhere Störungsreaktion und verschlechterte Stabilitätsmargen.
Numerische Effekte
Nachteilige numerische Effekte wie Koeffizientenquantisierung und Rundungsfehler verstärken sich mit steigender Abtastrate und manifestieren sich auf verschiedene Weise:
Integrative Prozesse haben unvorhersehbare Integrationsraten oder können unterbrochen werden: Beispiele für solche Prozesse sind Rampenfunktionsgeneratoren und PID-Regler-Integratoren. Am Beispiel der Rampengenerierung erzeugt die folgende Formel einen Rampenwert zum Zeitpunkt k durch Addition eines Deltawertes Δ = Integrationsrate / Abtastrate zum vorherigen Ausgang zum Zeitpunkt k - 1:
yk = yk-1 + Δ
| 1 kHz | 10 kHz | 100 kHz | |
| a1 = -1,991114 | a1 = -1,999111 | a1 = -1,999911 | |
| a2 = 0,991154 | a2 = 0,999112 | a2 = 0,999911 | |
Nur die Koeffizienten a1 und a2 sind relevant, da sie die Stabilität bestimmen und am anfälligsten für Rundungsfehler und Quantisierungseffekte sind. Beachten Sie, dass mit steigender Abtastrate die Anzahl der Ziffern, die nicht 9 sind, abnimmt. Das bedeutet, dass es viel weniger Ziffern gibt, die das Filterverhalten bestimmen. Wenn die Abtastrate weiter erhöht wird, nähert sich der Koeffizient a1 schließlich einem Wert von -2,0 und a2 einem Wert von 1,0. Irgendwann könnte die Quantisierung der Filterkoeffizienten zu einem Filter führen, dessen Frequenzgang unregelmäßig oder sogar instabil ist, d. h. der Ausgang oszilliert auch bei einem Eingang von Null mit großem Wert.

