
デジタル制御システムに慣れていない人は、サンプルレートが高いほど制御の忠実度が高いと考えています。 確かに、サンプルレートを上げると制御の忠実度は向上しますが、それは一定範囲までです。それ以上になると、制御は本質的にアナログになり、それ以上向上しません。 さらにサンプルレートを上げると、係数の量子化や丸め誤差などの有害な数値効果のために、制御の忠実度が実際には低下します。
このレポートでは、油圧サーボシステムの経験則として、最適なサンプルレートは油柱の固有振動数(またはその他の基本動的モード)として定義されるシステム帯域幅の 50 倍であることを示しています。ほとんどの MTS 油圧サーボシステムの帯域幅は 100Hz 以下なので、100×50=5kHz のサンプルレートで十分です。このサンプルレートを超えると、制御の忠実度はほとんど向上しません。
数値の影響で制御が劣化するサンプルレートは、数値の精度、信号の振幅や帯域幅、デジタルフィルターの折点周波数など多くの要因に依存するため、特定は困難です。徹底的な(つまり費用がかかる)試験によってのみ特定が可能です。
最適点を超えてサンプルレートを上げると、リアルタイムでハードウェアのコストが高くなります。また、機会損失のコストもあります。リアルタイムプロセッサの帯域幅の多くが制御の忠実性が向上しない計算に浪費されているため、AIC(適応的逆制御)のような忠実性を向上させる高度な制御アルゴリズムのための帯域幅はほとんど残っていません。
このレポートでは、検討対象をサンプルレートの制御に限定しています。コントローラには、データ収集サンプルレートなど、他のサンプルレートもあります。データ収集のサンプルレートを閉ループコントローラのサンプルレートよりもはるかに高く設定することには正当な理由があります。
次のテーマを検討します。
- サンプルレートに応じたコントロール忠実度
- レイテンシー(センサーのフィードバックを読み取ってからサーボ弁のコマンドを書き込むまでの遅延サンプル数)の関数としてのコントロール忠実度
- 数値的効果
このレポートで得られた結論を、ここで要約します。
- 大半の MTS 油圧サーボシステムに最適な制御サンプルレートは 5kHz です。 サンプルレートが高くても、ほとんどメリットはありません。
- 複数のリアルタイム プロセッサの負荷分散により高いサンプルレートを得るとレイテンシーが増加し、コントロールの忠実度が著しく低下します。
コントロールの忠実性は、様々な帯域幅、サンプルレート、レイテンシーの典型的な油圧サーボシステムの周波数応答解析を用いて分析・比較されました。
- 閉ループの周波数応答
- 外乱周波数応答
- 開ループ安定性の指標:ユニティゲインおよび -180度クロスオーバー周波数
油圧サーボシステムのモデルは以下のような特徴を持っています。
- 油圧アクチュエータは、解析ツールや Simulink のモデリングツールを開発するために何年も使われてきた「標準」設計でした。
- ペイロードは質量のみで、油柱の周波数(帯域幅)が 25、50、100Hz になるように質量を変化させました。
- サーボバルブの帯域幅は、ペイロードの帯域幅の 2 倍に制限されていました。
- フィードバック調整の帯域幅は、ペイロードの帯域幅の 10 倍に設定しました。
- 制御モードは変位でした。
- 制御アルゴリズムはPID(線形積分微分型)で、オートチューナーを用いてペイロードの帯域幅、サンプルレート、レイテンシーごとに最適なチューニングを行いました。最適化されたゲインには、変位誤差に対する比例ゲイン、デルタp安定化ゲイン、デルタpハイパスカットイン周波数が含まれています。
この油圧サーボモデルの詳細については、 Actuator Model.pdf 、 Actuator Transfer Functions.pdf 、 PID Transfer Functions.pdf を参照してください。
制御の忠実度(サンプルレートの関数として)
サンプルレートが制御の忠実度に与える影響を調べるために、制御サンプルレートを 2kHz、5kHz、10kHz、20kHz、システムの帯域幅を 25Hz、50Hz、100Hz に設定して分析しました。レイテンシーは、可能な限り最小の 1.5 コントローラ・サンプル期間としました。次のページでは、閉ループ、外乱、開ループの周波数応答を比較します。
このプロットを見ると、サンプルレートを 2kHz から 5kHz に上げることで、大半はサンプルレートが向上していることがわかります。それ以上の向上はほとんどありません。
帯域幅25Hzのシステムにおけるサンプルレートの影響
クローズドループの周波数応答は、サンプルレートを 2kHz から 5kHz に上げると、やや改善されます(よりフラットになります)。それ以外では、改善はほとんどありません。
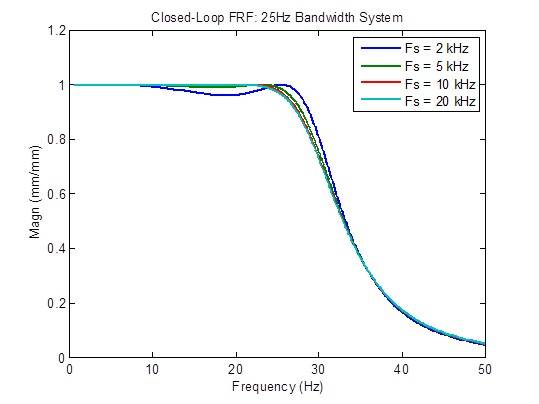
外乱応答は、サンプルレートを 2kHz から 5kHz に上げると、やや改善(減少)します。それ以外では、改善はほとんどありません。
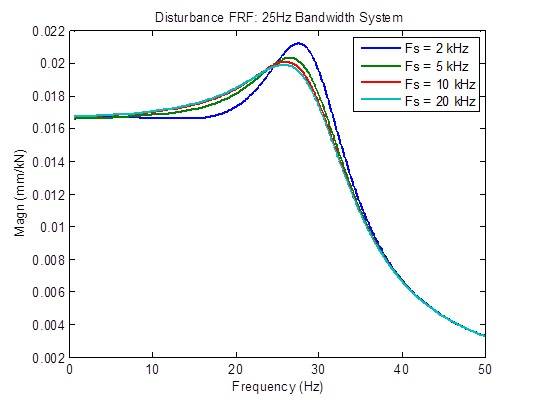
サンプルレートを 2kHz から 5kHz に上げると、開ループの周波数応答のピーキングがわずかに減少します。それ以外では、改善はほとんどありません。安定性の指標(クロスオーバー周波数)はほとんど変わりません。
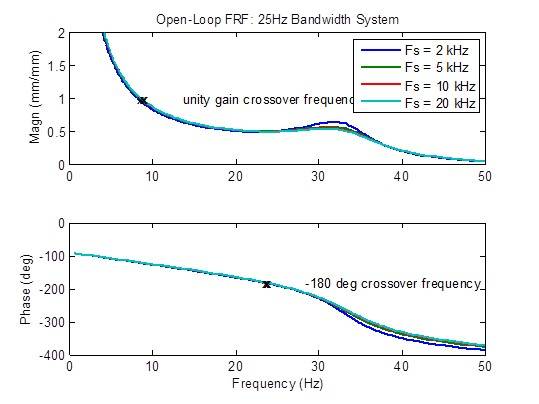
帯域幅50Hzのシステムにおけるサンプルレートの影響
クローズドループの周波数応答は、サンプルレートを 2kHz から 5kHz に上げると、少し改善されます(よりフラットになります)。それ以外では、改善はほとんどありません。
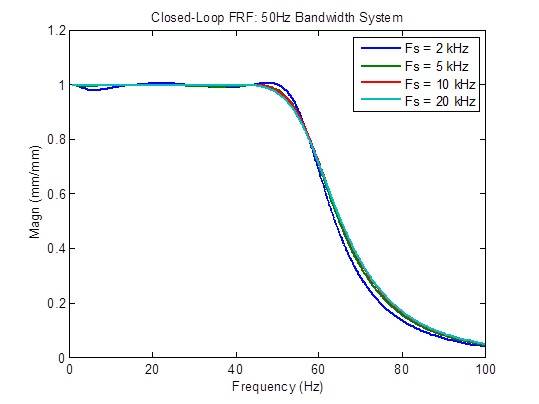
サンプルレートを 2kHz から 5kHz に上げた場合、外乱応答はある程度に改善(低減)され、5kHzから10kHzに上げた場合はやや改善されます。それ以外では、改善はほとんどありません。
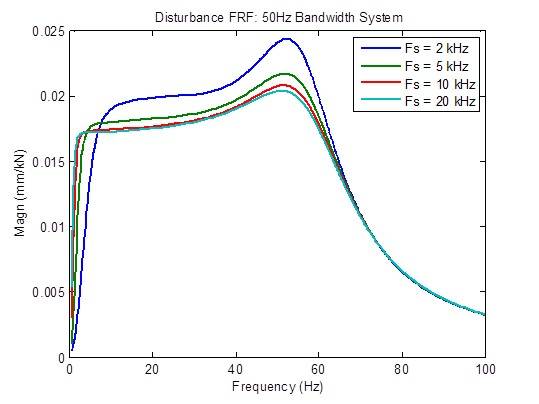
サンプルレートを 2kHz から 5kHz に上げると、開ループの周波数応答のピーキングがわずかに減少します。 安定性の指標(クロスオーバー周波数)も多少改善されています(より高い周波数)。 それ以外では、改善はほとんどありません。
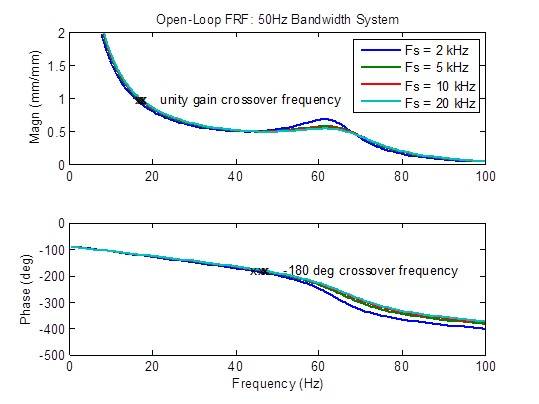
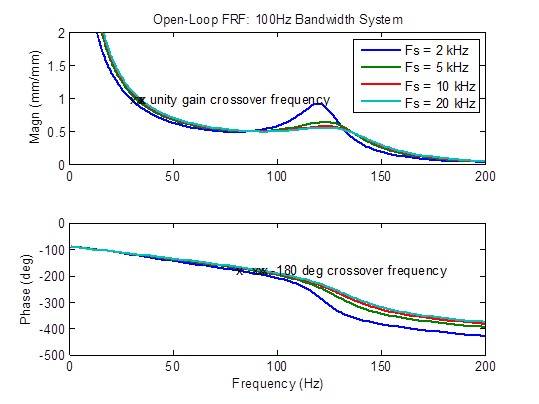
帯域幅100Hzのシステムにおけるサンプルレートの影響
クローズドループの周波数応答は、サンプルレートを 2kHz から 5kHz に上げると、著しく改善されます(よりフラットになります)。それ以外では、改善はほとんどありません。
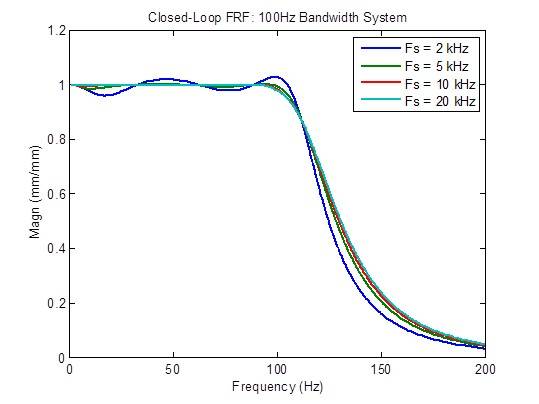
サンプルレートを 2kHz から 5kHz に上げた場合、外乱応答はある程度に改善(低減)され、5kHzから10kHzに上げた場合はやや改善されます。 それ以外では、改善はほとんどありません。
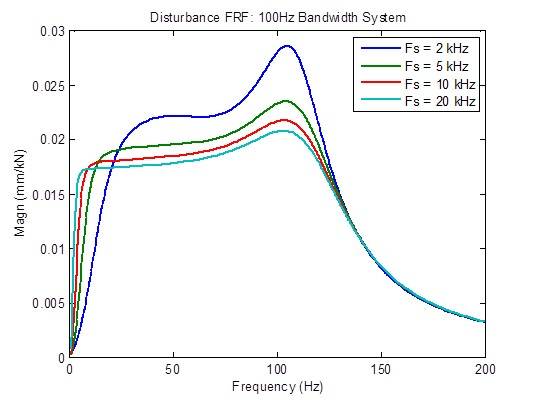
サンプルレートを 2kHz から 5kHz に上げると、開ループの周波数応答のピーキングがやや減少します。 安定性の指標(クロスオーバー周波数)も多少改善(周波数の上昇)されています。それ以外では、改善はほとんどありません。
制御の忠実度(レイテンシーの関数として)
サンプルレートを上げていくと、単体の実時間プロセッサに負荷がかかることがありますが、この問題は、プロセッサを追加して計算負荷を分担することで解決できます。
しかし、負荷分散により、センサーのフィードバックを読み取ってからサーボバルブのコマンドを書き込むまでの遅延サンプル数として定義されるレイテンシーは、次の式に従って増加します。
レイテンシー(サンプル) = プロセッサ数 + 0.5
0.5という数字は、デジタルからアナログへの変換による遅延です。可能な最小レイテンシーは 1.5 サンプルで、これはプロセッサがひとつしかない場合に発生します。プロセッサ数によるレイテンシーは、信号データを次のプロセッサに同期して渡す必要があるために発生します。
制御の忠実度に対するレイテンシーの影響を調べるために、帯域幅 100Hz とサンプルレート 10kHz のシステムを、1.5、4、10 サンプルのレイテンシーで分析しました。次のページでは、閉ループ、外乱、開ループの周波数応答を比較します。
以下のプロットは、レイテンシーが最小の 1.5 サンプルより増えると、制御の忠実度が著しく低下することを明確に示しています。 これは、高いサンプルレートを実現するためにプロセッサを追加することは必ずしも良いとは限らず、1 台のプロセッサの能力の範囲内で低いサンプルレートを使用した方が良い場合があることを示しています。
注記:今回、サンプルレート 10kHz、最大レイテンシー 10サンプルを選択したのは、MTS の競合他社が提供しているコントローラの仕様であるためです。 このセクションの最後のプロットでは、この競合他社のコントローラと、最適なサンプルレート 5kHz、最小レイテンシ 1.5 サンプルのコントローラを比較していますが、競合他社のコントローラは明らかに劣っています。
100Hzの帯域幅で10kHzのサンプルレートのシステムにおけるレイテンシーの影響
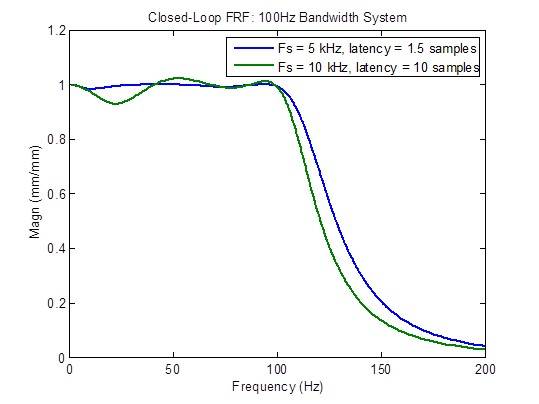
閉ループの周波数応答は、レイテンシーが最小の1.5サンプルより大きくなると、かなり劣化(フラットでなくなる)します。
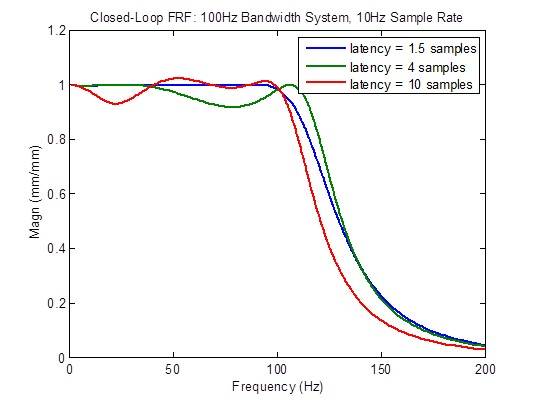
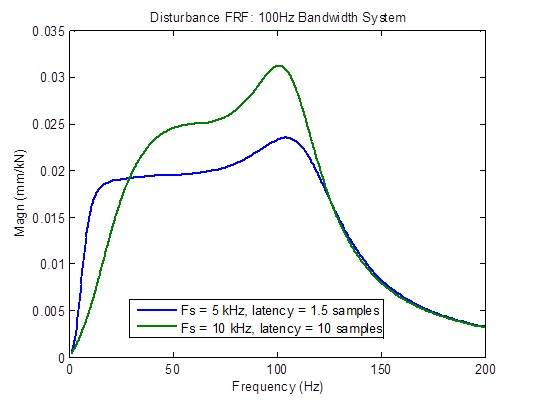
閉ドループの外乱応答は、レイテンシーが最小の1.5サンプルより大きくなると、かなり劣化(上昇)します。しかし、現時点では理由は不明ですが、低周波での改善が見られます。
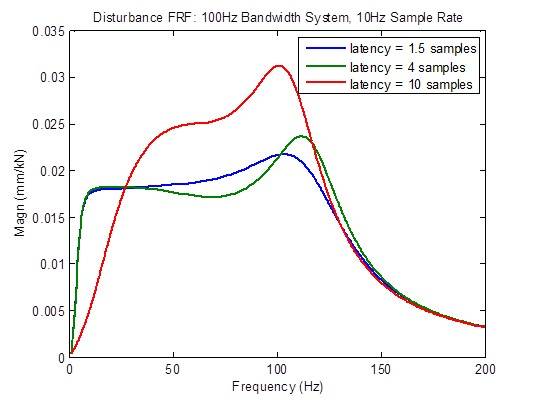
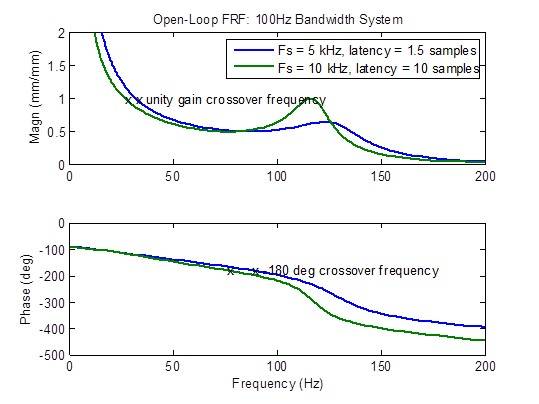
開ループの周波数応答は、レイテンシーが最小の 1.5 サンプルより大きくなると、かなり劣化(ピーク)します。安定性の指標(クロスオーバー周波数)は大幅に低下(低周波数で発生)します。
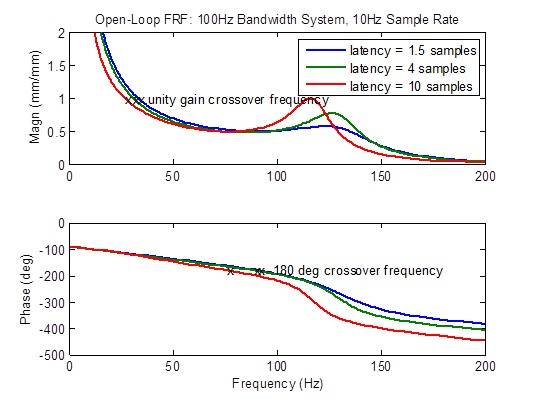
100Hz帯域のシステムで、レイテンシーの高い10kHzサンプルレートと レイテンシーの低い5kHzサンプルレートを比較すると、
MTSの競合他社は、レイテンシー1ミリ秒の10kHzサンプルレートコントローラを有することを示します(10サンプル@10kHz)。以下の周波数プロットでは、最小のレイテンシー(1.5 サンプル)で 5kHz のサンプルレートと比較して、あらゆる点で応答が劣っていることが明らかになっています。帯域幅の減少、閉ループ周波数応答の不均一化、外乱応答の増加、安定性マージンの低下などが挙げられます。
数値効果
係数の量子化や丸め誤差などの数値的な弊害は、サンプルレートの増加と共に悪化し、いくつかの形で現れます。
統合型のプロセスでは、統合率が予測できなかったり、行き詰まったりしました。 このようなプロセスの例としては、ランプ関数発生器や PID コントローラ積分器などが挙げられます。ランプ生成を例にとると、時刻 k において、前回の出力にデルタ値 Δ =積分率 / サンプルレート を加えることで、時刻 k - 1 のランプ値を生成します。
yk = yk-1 + Δ
| 1 kHz | 10 kHz | 100 kHz | |
| a1 = -1.991114 | a1 = -1.999111 | a1 = -1.999911 | |
| a2 = 0.991154 | a2 = 0.999112 | a2 = 0.999911 | |
a1 とa2 係数のみが、安定性を決定するものであり、丸め誤差や量子化効果の影響を最も受けやすいため重要です。サンプルレートが高くなると、9 以外の桁数が減ります。つまり、フィルターの応答を決定する桁数が非常に少ないのです。最終的には、サンプルレートをさらに上げると、係数a1 は -2.0 の値に近づき、a2 は 1.0 の値に近づきます。ある時点で、フィルターの係数を量子化すると、周波数応答が不安定になったり、入力がゼロでも出力が大きく振動するような不安定なフィルターになってしまいます。

