
Les personnes qui ne connaissent pas les systèmes de commande numérique pensent que plus le taux d’échantillonnage est élevé, meilleure est la fidélité de contrôle. Il est vrai que la fidélité de contrôle s’améliore avec l’augmentation du taux d’échantillonnage, mais seulement jusqu’à un certain point. Au-delà de ce point, le contrôle est essentiellement analogique et aucune autre amélioration ne survient. Si le taux d’échantillonnage augmente encore plus, la fidélité de contrôle se dégrade en réalité en raison d’effets numériques néfastes, tels que la quantification des coefficients et les erreurs d’arrondi.
Comme indiqué dans ce rapport, la règle de base pour les systèmes servohydrauliques veut que le taux d’échantillonnage optimal représente 50 fois la bande passante du système, définie comme la fréquence naturelle de la colonne d’huile (ou tout autre mode dynamique dominant). La bande passante de la plupart des systèmes servohydrauliques MTS est inférieure à 100 Hz ; par conséquent, un taux d’échantillonnage de 100 x 50 = 5 kHz est suffisant. Au-delà de ce taux d’échantillonnage, la fidélité de contrôle n’est pas ou peu améliorée.
Le taux d’échantillonnage auquel le contrôle se dégrade en raison d’effets numériques est difficile à déterminer, car il dépend de nombreux facteurs, tels que la précision numérique, l’amplitude et la bande passante du signal, les fréquences de coupure du filtre numérique,… Il ne peut être déterminé que par des essais exhaustifs (c’est-à-dire coûteux).
L’augmentation du taux d’échantillonnage au-delà du point optimal augmente le coût du matériel en temps réel. Il y a également un coût d’opportunité perdu : étant donné qu’une grande partie de la bande passante du processeur temps réel est gaspillée pour des calculs qui n’améliorent pas la fidélité de contrôle, il reste peu de bande passante pour les algorithmes de contrôle avancés qui améliorent la fidélité, tels que l’AIC (Commande adaptative inverse).
Ce rapport ne traite que du taux d’échantillonnage de contrôle. Il existe d’autres taux d’échantillonnage dans un contrôleur, tels que le taux d’échantillonnage de l’acquisition de données. De bonnes raisons peuvent justifier un taux d’échantillonnage d’acquisition de données beaucoup plus élevé que celui du contrôleur en boucle fermée.
Voici les sujets abordés :
- La fidélité de contrôle en fonction du taux d’échantillonnage
- La fidélité de contrôle en fonction de la latence (définie comme le nombre d’échantillons de retard entre la lecture de retour du capteur et l’écriture des commandes de la servovalve)
- Les effets numériques
Les conclusions de ce rapport sont les suivantes :
- Le taux d’échantillonnage de contrôle optimal de la plupart des systèmes servohydrauliques MTS est de 5 kHz. Des taux d’échantillonnage plus élevés ne présentent que peu ou pas d’avantages.
- Le fait d’obtenir des taux d’échantillonnage plus élevés en partageant la charge entre plusieurs processeurs temps réel augmente la latence, ce qui dégrade considérablement la fidélité de contrôle.
La fidélité de contrôle a été étudiée à l’aide de l’analyse de la réponse en fréquence d’un système servohydraulique classique ayant des bandes passantes, des taux d’échantillonnage et des latences différents et en comparant :
- La réponse en fréquence en boucle fermée
- La réponse en fréquence aux perturbations
- Les mesures de stabilité en boucle ouverte :fréquences de gain unité et de transfert à -180 degrés
Le modèle de système servohydraulique offrait les caractéristiques suivantes :
- Le vérin hydraulique était une conception « standard » utilisée depuis des années pour développer des outils d’analyse et de modélisation Simulink.
- La charge utile était constituée uniquement de masse, qui variait pour obtenir des fréquences de colonne d’huile (bandes passantes) de 25, 50 et 100 Hz.
- La bande passante de la servovalve était limitée à deux fois la bande passante de la charge utile.
- La bande passante de conditionnement de retour était fixée à 10 fois la bande passante de la charge utile.
- Le mode de contrôle était le déplacement.
- L’algorithme de contrôle était de type PID (proportionnel, intégral, dérivé) avec un réglage optimisé pour chaque bande passante, taux d’échantillonnage et latence de la charge utile à l’aide d’un syntoniseur automatique. Les gains optimisés comprenaient : un gain proportionnel sur l’erreur de déplacement, un gain de stabilisation de Delta P et une fréquence de déclenchement du passe-haut Delta P.
Pour plus de détails sur ce modèle servohydraulique, voir Actuator Model.pdf, Actuator Transfer Functions.pdf et PID Transfer Functions.pdf.
Fidélité de contrôle (en fonction du taux d’échantillonnage)
Pour déterminer l’effet du taux d’échantillonnage sur la fidélité de contrôle, le système a été analysé avec des taux d’échantillonnage de contrôle de 2 kHz, 5 kHz, 10 kHz et 20 kHz, et des bandes passantes du système de 25 Hz, 50 Hz et 100 Hz. La latence était la plus faible possible : 1,5 fois la période d’échantillonnage du contrôleur. Les pages suivantes présentent des comparaisons de la réponse en fréquence en boucle fermée, aux perturbations et en boucle ouverte.
Les graphiques montrent clairement que la plupart des avantages de l’augmentation du taux d’échantillonnage sont obtenus en augmentant le taux d’échantillonnage de 2 kHz à 5 kHz. Au-delà, les améliorations sont minimes.
Effet du taux d’échantillonnage sur un système à bande passante de 25 Hz
La réponse en fréquence en boucle fermée s’améliore quelque peu (plus plate) lorsque le taux d’échantillonnage passe de 2 kHz à 5 kHz. Au-delà, les améliorations sont minimes :
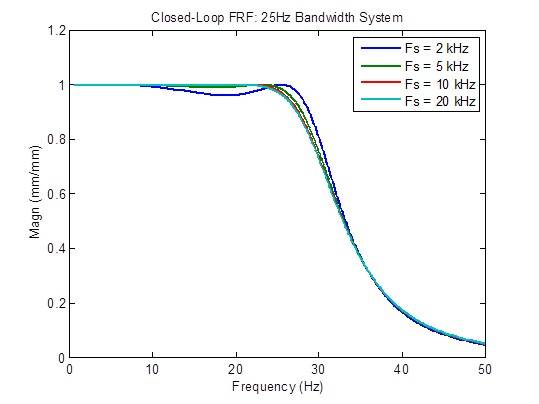
La réponse aux perturbations s’améliore quelque peu (réduite) lorsque le taux d’échantillonnage passe de 2 kHz à 5 kHz. Au-delà, les améliorations sont minimes :
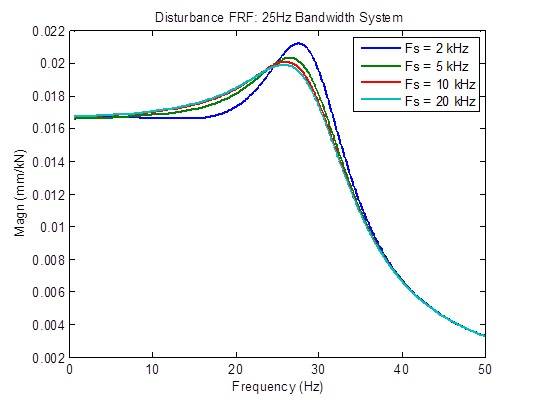
Il y a une légère réduction du pic de la réponse en fréquence en boucle ouverte lorsque le taux d’échantillonnage passe de 2 kHz à 5 kHz. Au-delà, les améliorations sont minimes. Les mesures de stabilité (fréquences de transfert) n’ont pratiquement pas changé :
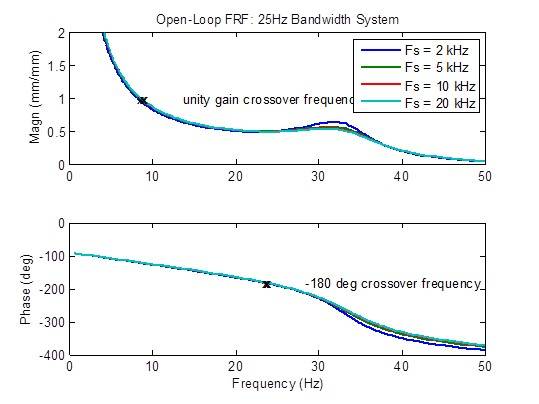
Effet du taux d’échantillonnage sur un système à bande passante de 50 Hz
La réponse en fréquence en boucle fermée s’améliore quelque peu (plus plate) lorsque le taux d’échantillonnage passe de 2 kHz à 5 kHz. Au-delà, les améliorations sont minimes :
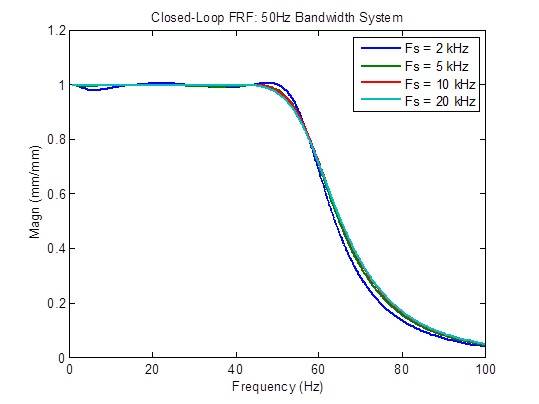
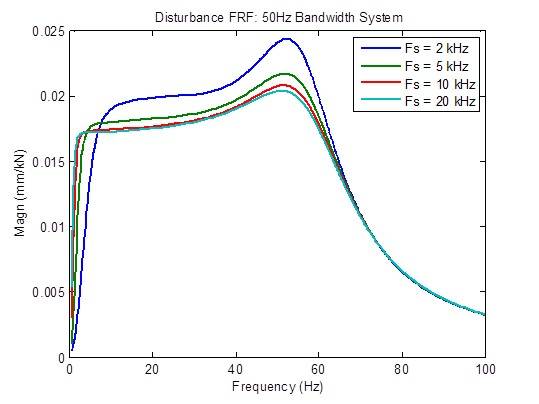
La réponse aux perturbations s’améliore moyennement (réduite) lorsque le taux d’échantillonnage passe de 2 kHz à 5 kHz et quelque peu lorsqu’il passe de 5 kHz à 10 kHz. Au-delà, les améliorations sont minimes :
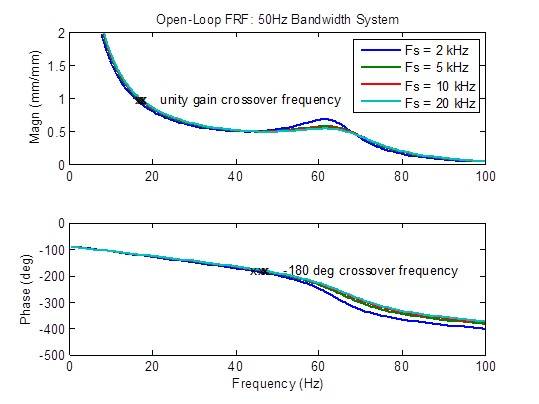
Il y a une légère réduction du pic de la réponse en fréquence en boucle ouverte lorsque le taux d’échantillonnage passe de 2 kHz à 5 kHz. Les mesures de stabilité (fréquences de transfert) se sont également quelque peu améliorées (fréquence plus élevée). Au-delà, les améliorations sont minimes :
Effet du taux d’échantillonnage sur un système à bande passante de 100 Hz
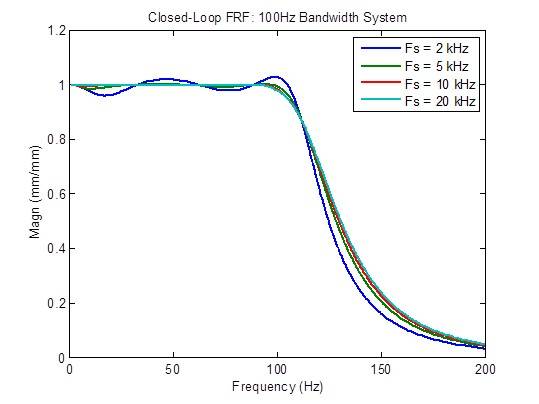
La réponse en fréquence en boucle fermée s’améliore significativement (plus plate) lorsque le taux d’échantillonnage passe de 2 kHz à 5 kHz. Au-delà, les améliorations sont minimes :
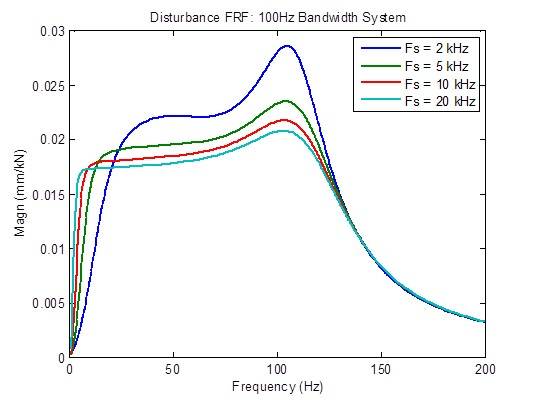
La réponse aux perturbations s’améliore moyennement (réduite) lorsque le taux d’échantillonnage passe de 2 kHz à 5 kHz et quelque peu lorsqu’il passe de 5 kHz à 10 kHz. Au-delà, les améliorations sont minimes :
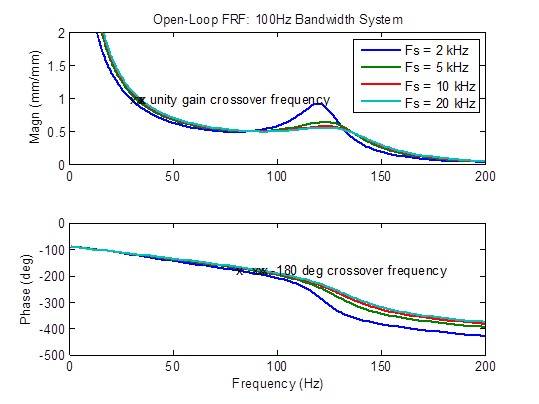
Il y a une réduction modérée du pic de la réponse en fréquence en boucle ouverte lorsque le taux d’échantillonnage passe de 2 kHz à 5 kHz. Les mesures de stabilité (fréquences de transfert) se sont également moyennement améliorées (fréquence plus élevée).Au-delà, les améliorations sont minimes :
Fidélité de contrôle (en fonction de la latence)
L’augmentation du taux d’échantillonnage surchargera à un moment donné un seul processeur temps réel ; ce problème peut être résolu en ajoutant d’autres processeurs et en partageant la charge de calcul entre eux.
Cependant, le partage de charge augmente la latence, qui est définie comme le nombre d’échantillons de retard entre la lecture de retour du capteur et l’écriture des commandes de la servovalve, selon la formule suivante :
Latence (échantillons) = nombre de processeurs + 0.5
Le chiffre 0,5 correspond au retard dû à la conversion du numérique vers l’analogique. La latence minimale possible est de 1,5 échantillon, ce qui se produit lorsqu’un seul processeur est présent. La latence due au nombre de processeurs résulte de la nécessité de synchroniser le passage des données de signal d’un processeur au suivant.
Pour déterminer l’effet de la latence sur la fidélité de contrôle, un système avec une bande passante de 100 Hz et un taux d’échantillonnage de 10 kHz a été analysé avec des latences de 1,5, 4 et 10 échantillons. Les pages suivantes présentent des comparaisons de la réponse en fréquence en boucle fermée, aux perturbations et en boucle ouverte.
Les graphiques ci-dessous montrent clairement que la fidélité de contrôle se dégrade considérablement lorsque la latence augmente au-delà de la valeur minimale de 1,5 échantillon. Cela démontre que l’ajout de processeurs pour obtenir un taux d’échantillonnage élevé n’est pas nécessairement une bonne chose et qu’il vaut mieux utiliser un taux d’échantillonnage inférieur, qui soit dans les limites de la capacité d’un seul processeur.
N.B. : la raison qui explique le choix d’un taux d’échantillonnage de 10 kHz et d’une latence maximale de 10 échantillons pour cette analyse tient au fait qu’il s’agit des spécifications d’un contrôleur proposé par un concurrent de MTS. Les derniers graphiques de cette section comparent le contrôleur de ce concurrent avec un contrôleur ayant un taux d’échantillonnage optimal de 5 kHz et une latence minimale de 1,5 échantillon ; le contrôleur du concurrent est nettement inférieur.
Effet de la latence sur un système à bande passante de 100 Hz avec un taux d’échantillonnage de 10 kHz
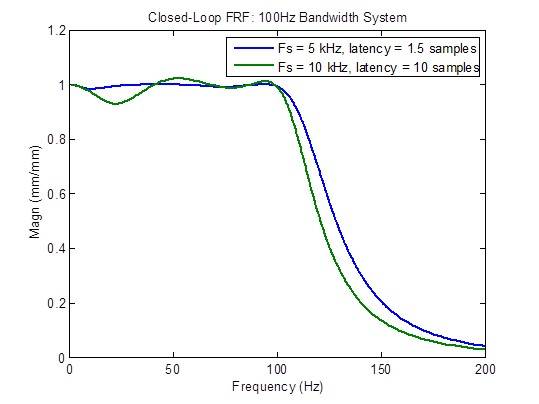
La réponse en fréquence en boucle fermée se dégrade considérablement (moins plate) lorsque la latence est supérieure à la valeur minimale de 1,5 échantillon :
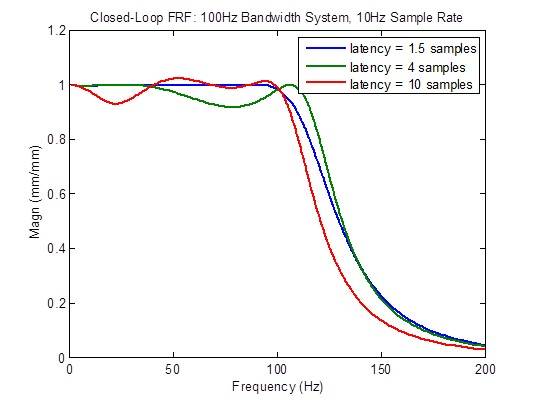
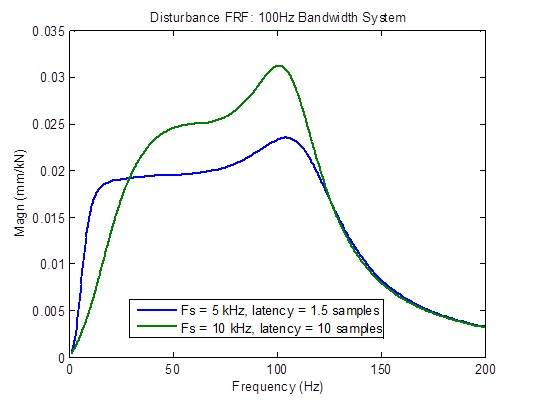
La réponse aux perturbations se dégrade considérablement (plus élevée) lorsque la latence est supérieure à la valeur minimale de 1,5 échantillon. Cependant, il y a une amélioration dans les fréquences basses pour des raisons inconnues à l’heure actuelle :
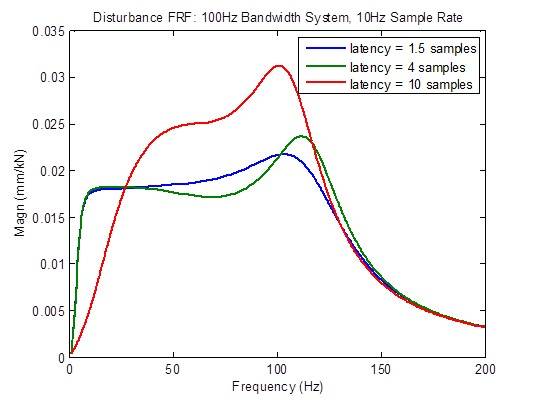
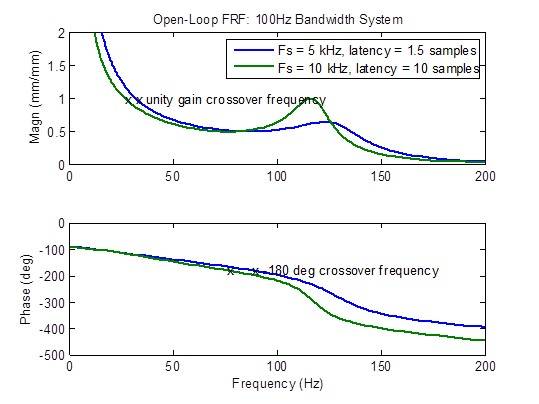
La réponse en fréquence en boucle ouverte se dégrade considérablement (apparition de pics) lorsque la latence est supérieure à la valeur minimale de 1,5 échantillon. Les mesures de stabilité (fréquences de transfert) se dégradent considérablement (apparaissent à une fréquence plus basse) :
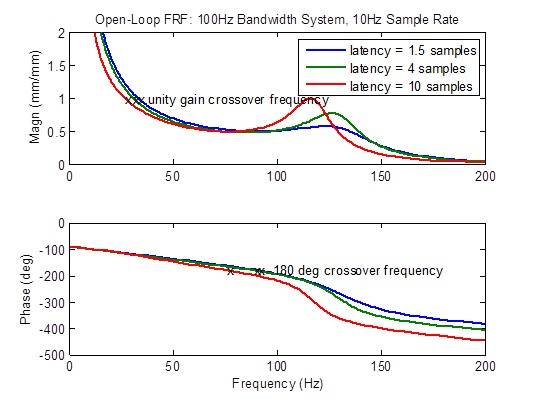
Comparaison entre un système à bande passante de 100 Hz avec un taux d’échantillonnage de 10 kHz à latence élevée et avec un taux d’échantillonnage de 5 kHz à latence minimale
Un concurrent de MTS prétend avoir un contrôleur de taux d’échantillonnage de 10 kHz avec une latence de 1 milliseconde (10 échantillons à 10 kHz). Les graphiques de fréquence ci-dessous montrent clairement une réponse inférieure à tous égards par rapport à un taux d’échantillonnage de 5 kHz avec une latence minimale (1,5 échantillon) : bande passante réduite, réponse en fréquence en boucle fermée non plate, réponse aux perturbations plus élevée et marges de stabilité dégradées.
Effets numériques
Les effets numériques néfastes, tels que la quantification des coefficients et les erreurs d’arrondi s’aggravent avec l’augmentation du taux d’échantillonnage et se manifestent de plusieurs manières :
Les processus intégratifs ont des taux d’intégration imprévisibles ou peuvent se bloquer : parmi les exemples de tels processus figurent les générateurs de rampe et les intégrateurs de contrôleurs PID. En prenant la génération de rampe comme exemple, la formule ci-dessous génère une valeur de rampe à l’instant k en ajoutant une valeur delta Δ = taux d’intégration / taux d’échantillonnage à la sortie précédente à l’instant k - 1 :
yk = yk-1 + Δ
| 1 kHz | 10 kHz | 100 kHz | |
| a1 = -1,991114 | a1 = -1,999111 | a1 = -1,999911 | |
| a2 = 0,991154 | a2 = 0,999112 | a2 = 0,999911 | |
Seuls les coefficients a1 et a2 sont intéressants, car ce sont eux qui déterminent la stabilité et qui sont les plus sensibles aux erreurs d’arrondi et aux effets de quantification. Notez que lorsque le taux d’échantillonnage augmente, le nombre de chiffres autres que 9 diminue. Cela signifie qu’il y a beaucoup moins de chiffres qui déterminent la réponse du filtre. Finalement, plus le taux d’échantillonnage augmente, plus le coefficient a1 tend vers une valeur de -2,0 et a2 vers une valeur de 1,0. A un moment donné, la quantification des coefficients de filtre peut aboutir à un filtre dont la réponse en fréquence est erratique ou même instable, où la sortie oscille avec une valeur élevée, même avec une entrée nulle.

